Sesión 7
Curso: R Aplicado a los Proyectos de Investigación
Percy Soto-Becerra, M.D., M.Sc(c)
InkaStats Data Science Solutions | Medical Branch
2022-10-17

Revisando inferencia estadística clásica frecuentista
Agenda
Revisando inferencia estadística clásica frecuentista
Inferencia estadística
La meta es reportar un estimado puntual y su incertidumbre asociada.
Estimación puntual
La estimación puntual es el valor más probable del parámetro que podemos “adivinar” en base a los datos de la muestra que tenemos.
Que sea nuestra mejor apuesta no lo hace lo mejor del mundo. Es solo lo que podemos decir con lo que tenemos, nada más ni nada menos.
Incertidumbre asociada
Siempre hay incertidumbre asociada a la estimación, podemos indicar qué tan incierta es nuestra estimación a través de dos procedimientos:
Prueba de hipótesis: Valor p actúa como una medida de incertidumbre que, asumiendo ciertos puntos de corte, me permite tomar postura sobre el parámetro.Estimación de intervalo: Intervalo de confianza da rango de valores plausibles que podrían ser compatibles con el valor del parámetro si y solo si el intervalo captuar el verdadero valor (recordar: ¡siempre existe la posibilidad de que no lo capture!).
El parámetro
Independientemente de la distribución de la variable respuesta, lo que queremos estimar es una medida de resumen de esta variable en la población: media, mediana, difernecia de medias, diferencia de medianas, razón de odds, razón de riesgos, etc.
- Este valor es fijo y único: el valor verdadero del parámetro.
- No se distribuye ni nada por el estilo, es el valor único para todo el grupo de individuos.
- Sin embargo, los valores individuales de la población (que luego se resumen) son los que lo generan.
- Estos valores individuales si tienen un mecanismo generador que puede ser modelado como una distribución de probabilidades.
El estadístico
En cada muestra, en cambio, el estadístico que se calcula (media, mediana, diferencia de medias, razón de odds, etc.) no es fijo.
- Cada vez que saques una muestra, este estadístico cambiará.
- Cambia porque, por azar, te tocaron individuos diferentes de la misma población.
- A veces el estadístico tendrá valores muy cercanos al parámetro que quiero estimar, otras veces estará muy alejado (“muestras de mala suerte”).
- Con los datos de mi estudio, nunca sabré qué muestra me tocó (la de buena o mala suerte).
Lógica frecuentista
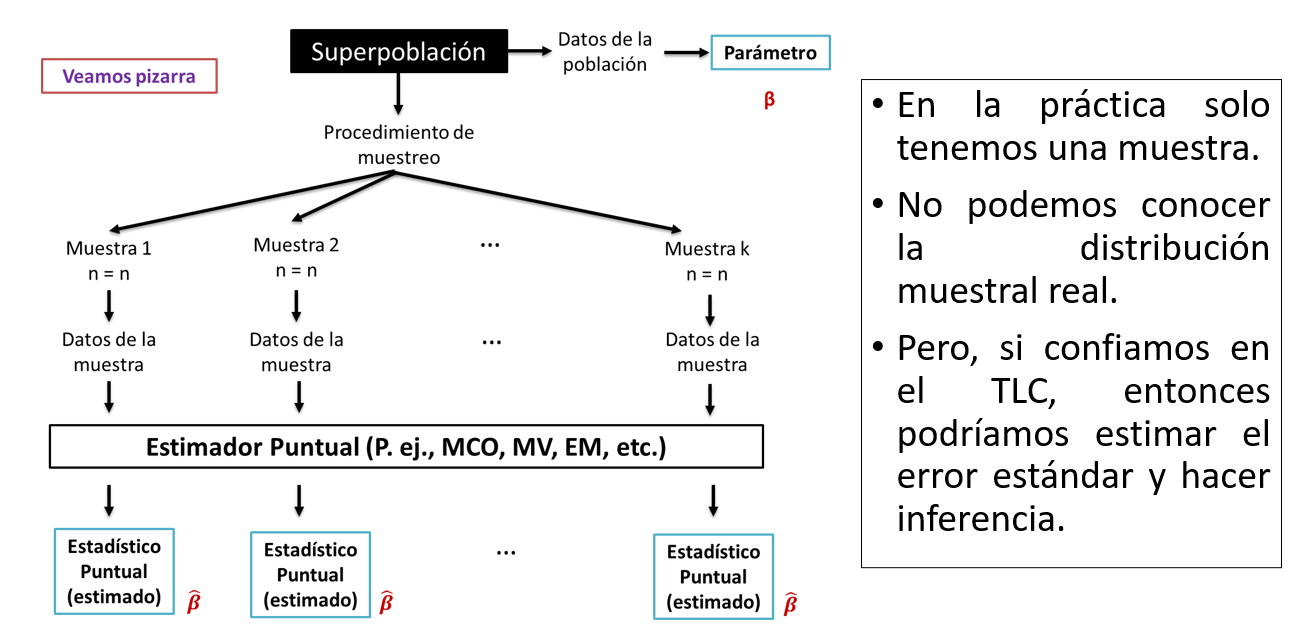
La distribución muestral es lo importante!
En realidad no importa qué distribución tenga la variable respuesta, en cuanto podamos estimar bien el parámetro y su incertidumbre asociada a la estimación.
Para estimar bien el parámetro requerimos un estimador que sea insesgado.
Insesgado siempre:
Estimador insesgadoInsesgado si y solo si n es grande:
Estimador consistente.
Para estimar bien la incertidumbre necesitamos conocer la distribución de los estadísticos que genera el estimador.
- La distribución de todas las muestras posibles siga cierto comportamiento!
Parámetro, Estimador, Estimado:
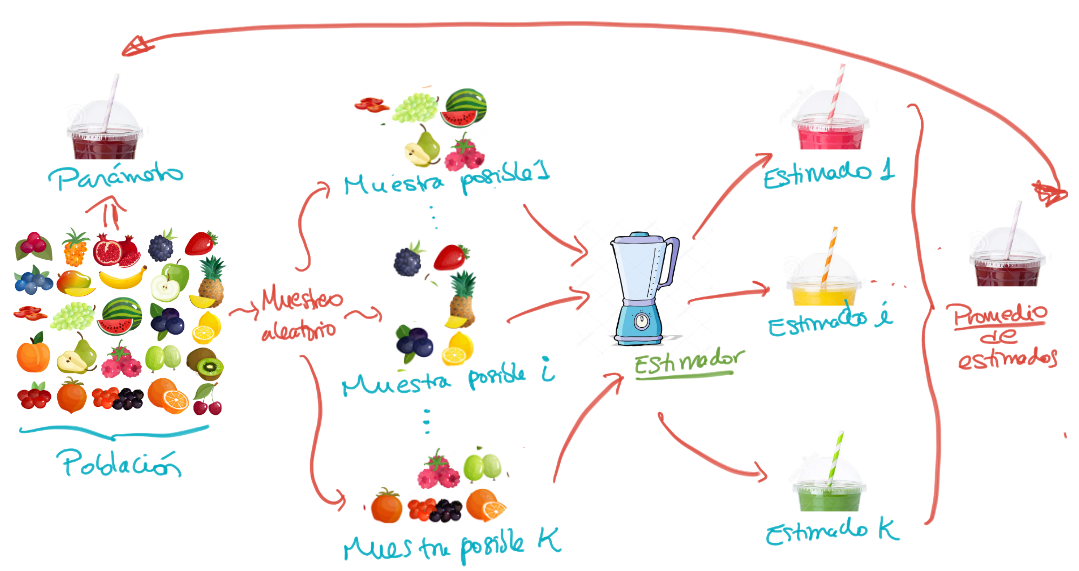
La distribución muestral es lo importante
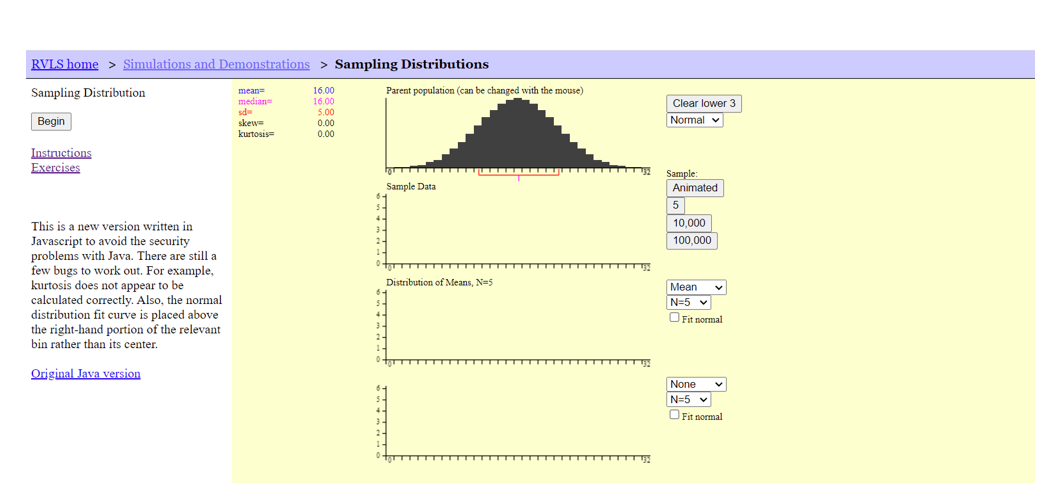
¿Cómo obtener el error estándar?
En la práctica habitual, no es posible calcular el error estándar real
Si tuviera todas las muestras posibles, lo calcularía directamente.
En la práctica real, solo tengo una muestra (ni dos, ni tres, ni mucho menos todas…)
No podemos dibujar la distribución muestral real.
Mucho menos calcular la varianza / error estándar “real” del estimador (por el motivo anterior)
¿Cómo obtener el error estándar? (cont.)
En la práctica habitual, sí podemos estimar el error estándar.
- Si se cumplen ciertos supuestos, podemos estimar el error estándar basándonos en los datos de una sola muestra:
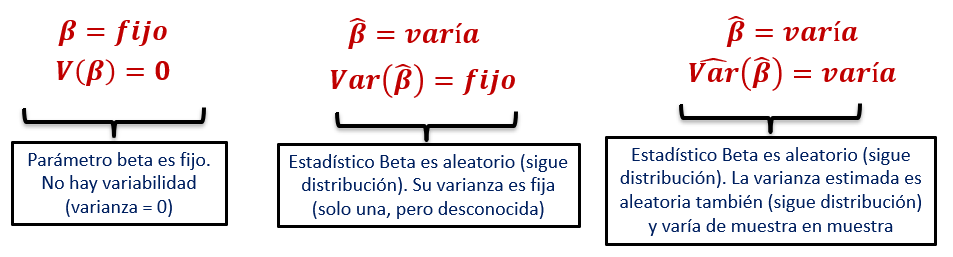
Error estándar, valor p e IC.
Cálculo del valor p e IC requieren de la varianza del estimador.
- Como no es posible obtenerlo, se usa una estimación del varianza del estimador (de su raíz cuadrada): Error estándar.
Sea β una
diferencia de mediasde interés.
- Valor p para ˆβ:
Tcalculado=ˆβ−β0SE(ˆβ)
- Luego, se asume que si H0 es cierta y TLC se cumple, el T calculado sigue una distribución t de Student.
- IC para ˆβ:
Límite del IC=ˆβ±t1−α/2, glSE(ˆβ)
- Aquí también se asume que si TLC se cumple, la distribución t permite construir un IC.
¿Qué pasa si estimamos mal el error estándar del estimador?
Si estimamos bien el error estándar y, además, asumimos la distribución apropiada, entonces el valor p y el IC serán válidos.
Eso significa que la cobertura nominal del IC a la cobertura real del IC.
Del mismo modo, la significancia nominal del valor p = a la significancia real del valor p.
Si lo estimamos mal (o asumimos una distribución inapropiada), entonces el valor p y el IC serán sesgadas.
Generará problemas de cobertura.
Las coberturas o significancias nominales serán diferentes a las reales
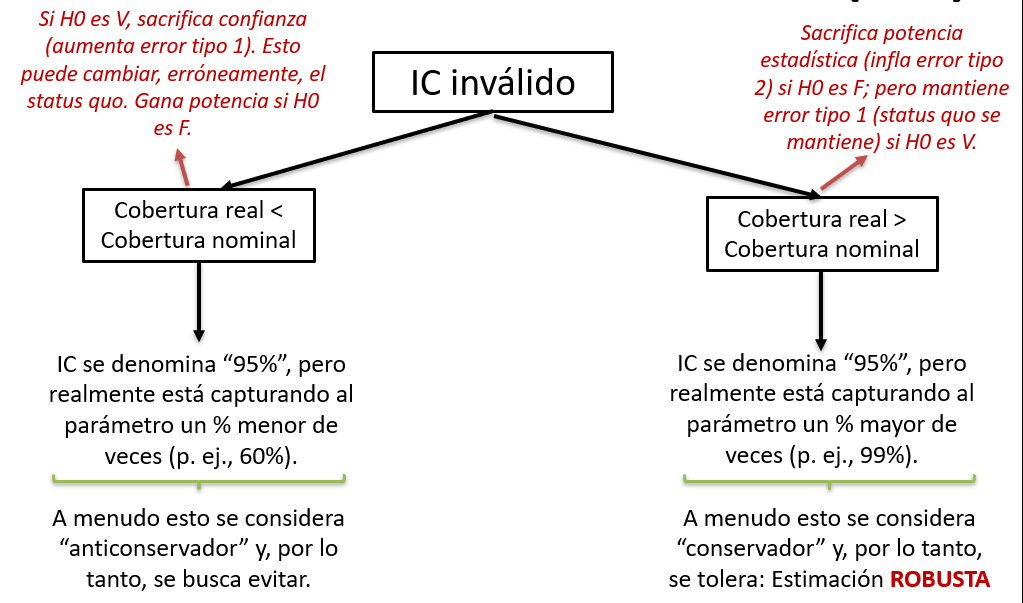
Este sesgo de los valores p / IC puede ser anticonservador y, por lo tanto, ser considerado inválido.
O ser conservador y, por tanto, ser considerado robusto.
IC válido versus IC inválido
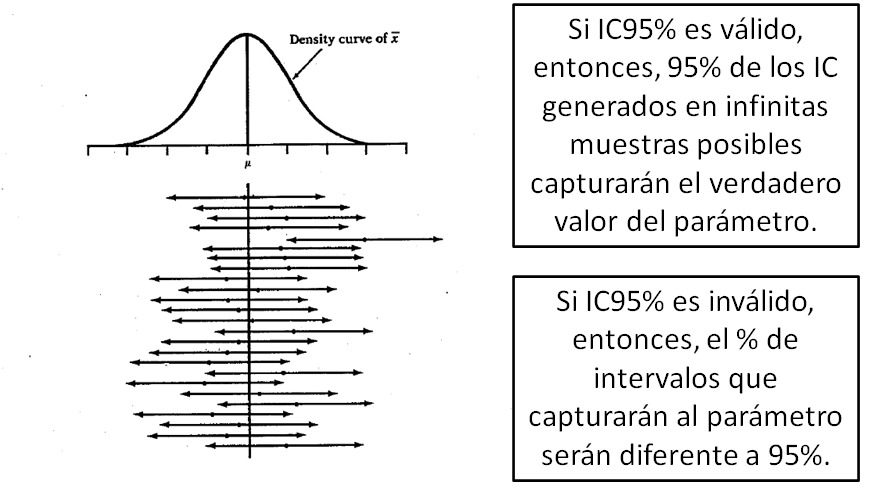
IC válido versus IC inválido (cont.)
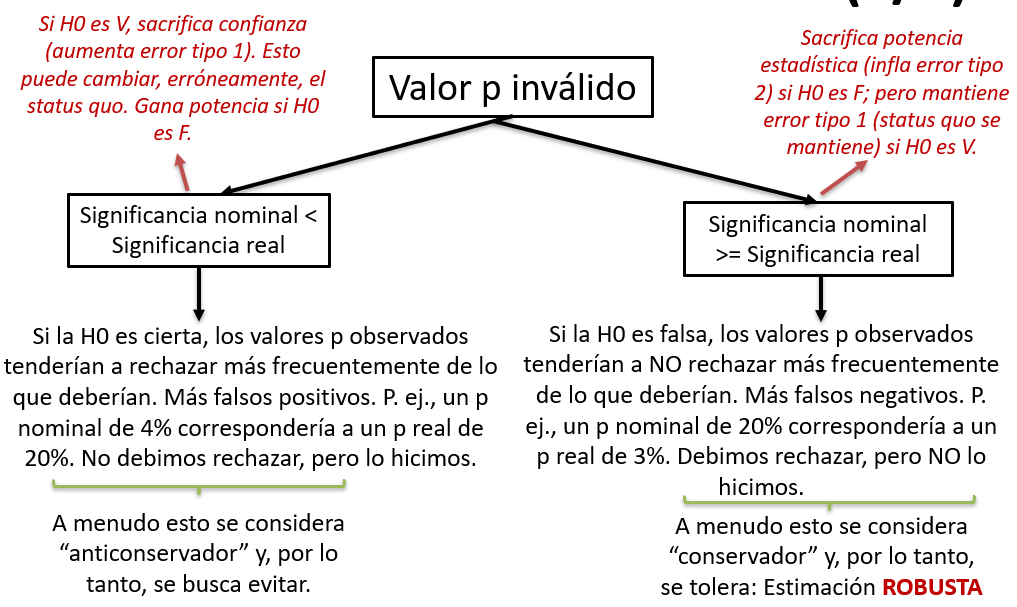
Valor p válido versus inválido (cont.)
¿Cómo podemos obtener una estimación válida del error estándar?
Cuando los supuestos se cumplen, podemos asumir distribuciones conocidas: comportamiento asintótico conocido del estimador.
Cuando algunos supuestos no se cumplen, podemos:
Usar métodos robustos de estimacion del error estándar.
Usar remuestreo (bootstrapping o pruebas de permutación).
¿Estimación robusta del error estándar?
Estimación del error estándar que generará resultados “conservadores”
Es decir, se mantiene la tasas de error tipo 1 si H0 es V.
A pesar de que si H0 es F, se pierda potencia.
Es decir, las significancias / coberturas reales son:
Iguales a las nominales (en el mejor de los casos).
Mayores a las nominales (en el peor de los casos).
Aunque podemos tolerar que las significancias / coberturas reales sean mayores que las nominales:
Un gran número de veces serán iguales, se alcanzará la situación ideal.
Cuando no se alcanza la situación ideal, hay cierta pérdida de eficiencia en el uso de los datos, ya que se está sacrificando potencia estadística.
¿Bootstrapping?
Procedimiento de remuestreo.
Se toman muestras bootstrap:
Muchas muestras con remplazo de tamaño n.
Se construye una distribución empírica del estadístico.
Podemos usar esta distribución empírica como una aproximación de la distribución real del estadístico y estimar de esta el error estándar.
¿Pruebsa de permutación?
Asumiendo que no hay diferencias entre los grupos, hubiera dado igual a quién le tocó o no el tratamiento.
Podemos permutar el orden de los individuos manteniendo fijos los tratamiento.
Podemos ver todos los órdenes posibles y preguntarnos qué tan probable es encontrar el resulado de nuestra muestra.
Este valor de probabilidad es equivalente al valor p y funciona para probar hipótesis.
Nuestro turno
Descargue la carpeta denominada taller06 disponible en la carpeta compartida.
Abra el proyecto denominado taller06.Rproj
Complete y ejecute el código faltante en los chunk de código.
Una vez culmine todo el proceso, renderice el archivo .qmd.
https://github.com/psotob91
percys1991@gmail.com

R Aplicado a los Proyectos de Investigación - Sesión 7