Sesión 8

Curso: R Aplicado a los Proyectos de Investigación

Percy Soto-Becerra, M.D., M.Sc(c)

InkaStats Data Science Solutions | Medical Branch

2022-10-19

  https://github.com/psotob91

Introducción al modelado de regresión

Agenda

  1. Introducción al modelado de regresión

  2. Modelo de Regresión Lineal Simple

  3. Regresión Lineal Simple en R

  4. Regresión Lineal Múltiple

  5. Regresión Lineal Múltiple en R

  6. Evaluación de Supuestos

Análisis de regresión

Conjunto de técnicas estadística para estimar la relación entre variables.

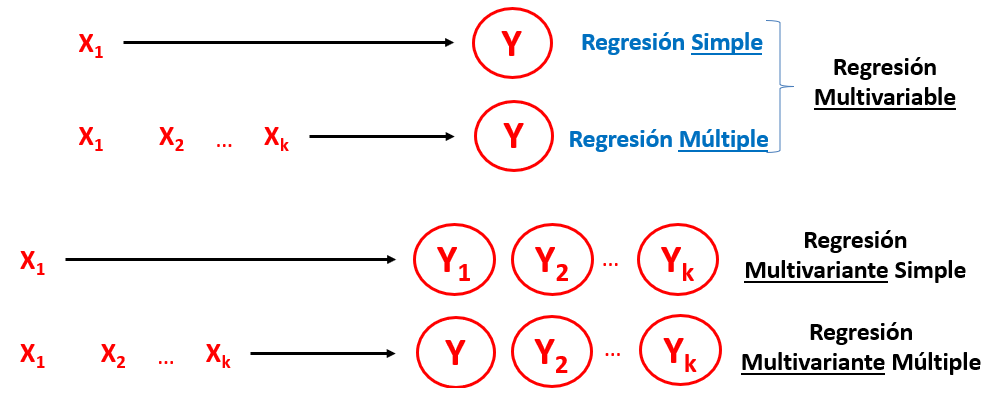
Modelos de regresión multivariable

Los modelos de regresión multivariable modelan una sola variable dependiente en función de una o más variables independientes.

  • El desenlace define el tipo de regresión multivariable.

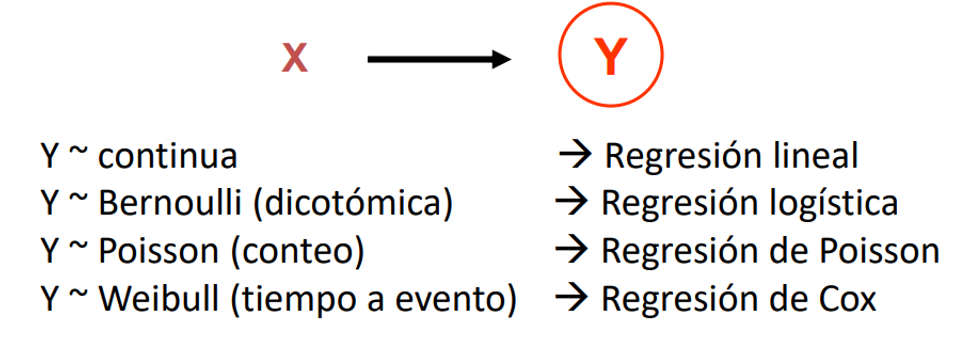
¿Para qué usamos los modelos de regresión?

  • Según STRATOS podemos usar regresión para 3 propósitos diferentes:

    • Descripción*

    • Predicción

    • Explicación

Propósitos del modelamiento


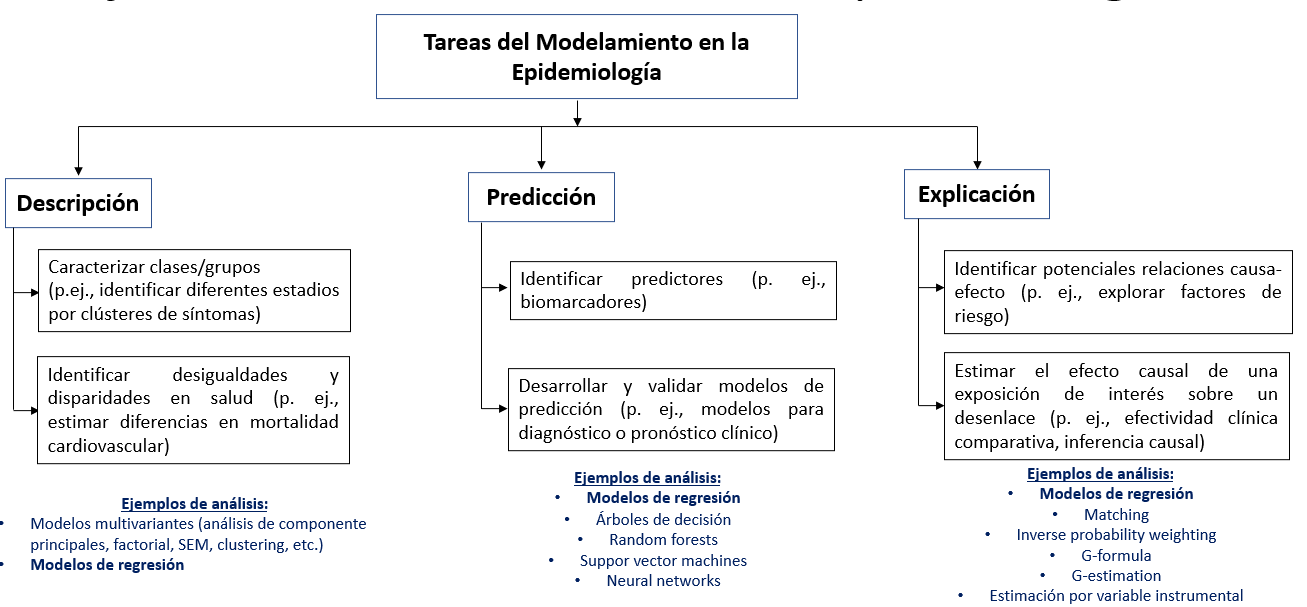
Clasificación inspirado en: Miguel A. Hernán, John Hsu & Brian Healy (2019) A Second Chance to Get Causal Inference Right: A Classification of Data Science Tasks, CHANCE, 32:1, 42-49, DOI: 10.1080/09332480.2019.1579578

Propósitos del modelamiento (cont.)


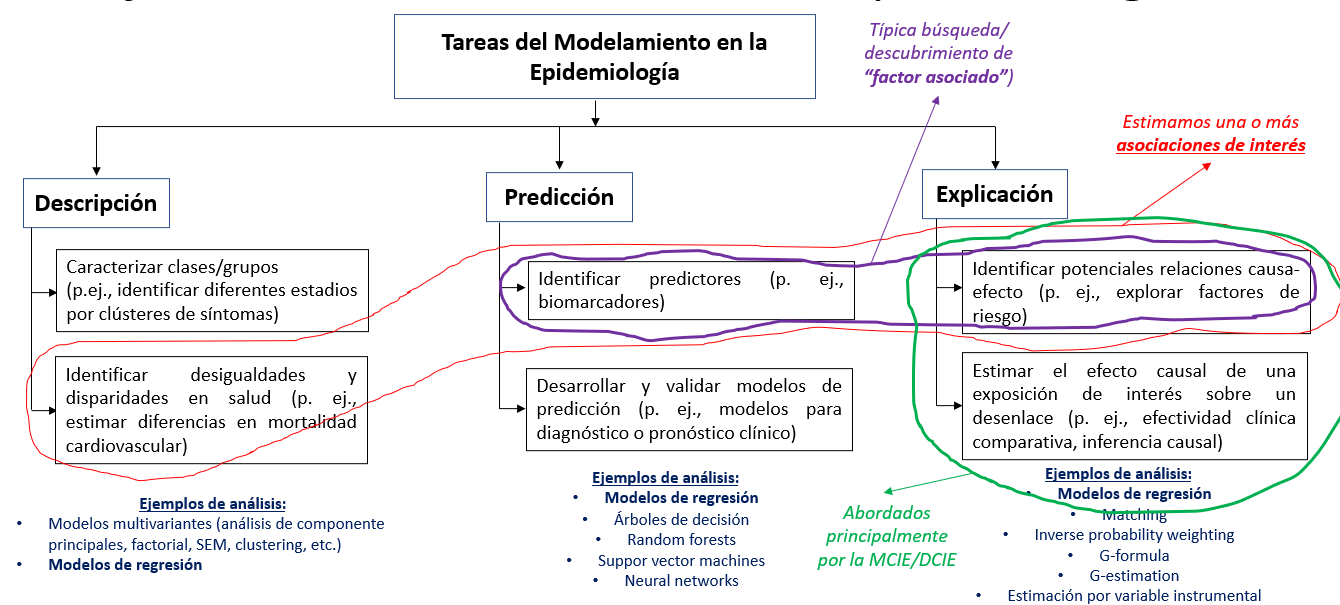
Clasificación inspirado en: Miguel A. Hernán, John Hsu & Brian Healy (2019) A Second Chance to Get Causal Inference Right: A Classification of Data Science Tasks, CHANCE, 32:1, 42-49, DOI: 10.1080/09332480.2019.1579578

¿Para qué usamos los modelos de regresión? (cont.)

  • Este curso se centrará solamente en algunas aplicaciones.

  • No abordaremos modelos de regresión para desarrollar modelos o reglas de predicción clínica.

  • Tampoco para métodos de inferencia causal robusta.

  • Descripción
  • Explicación
  • Predicción
  • Evaluación de la magnitud de desigualdades, magnitud de brechas, etc.
  • “Factores asociados..:” No necesariamente importa que los factores sean causales.
  • “Efecto / Efectividad / Impacto”: Busca estimar efectos causales.
  • Explorar potenciales factores causales… (puede clasificarse dentro de descripción)
  • Factores pronóstico o predictores de…“: Identifican predictores de interés que luego alimenten mdelos predictivos.
  • Modelos de predicción: Predicción para diagnóstico y pronóstico.

Modelo de Regresión Lineal Simple

Agenda

  1. Introducción al modelado de regresión

  2. Modelo de Regresión Lineal Simple

  3. Regresión Lineal Simple en R

  4. Regresión Lineal Múltiple

  5. Regresión Lineal Múltiple en R

  6. Evaluación de Supuestos

Regresión Lineal

Método estadístico que modela la relación entre una variable continua (dependiente) y otras variables (independientes).

Relación entre dos variables

  • Y es variable resultado (outcome), respuesta o dependiente.

  • X es una variable explicativa, predictora o regresora.

  • En la figura, a mayor valor de X, mayor valor de Y.

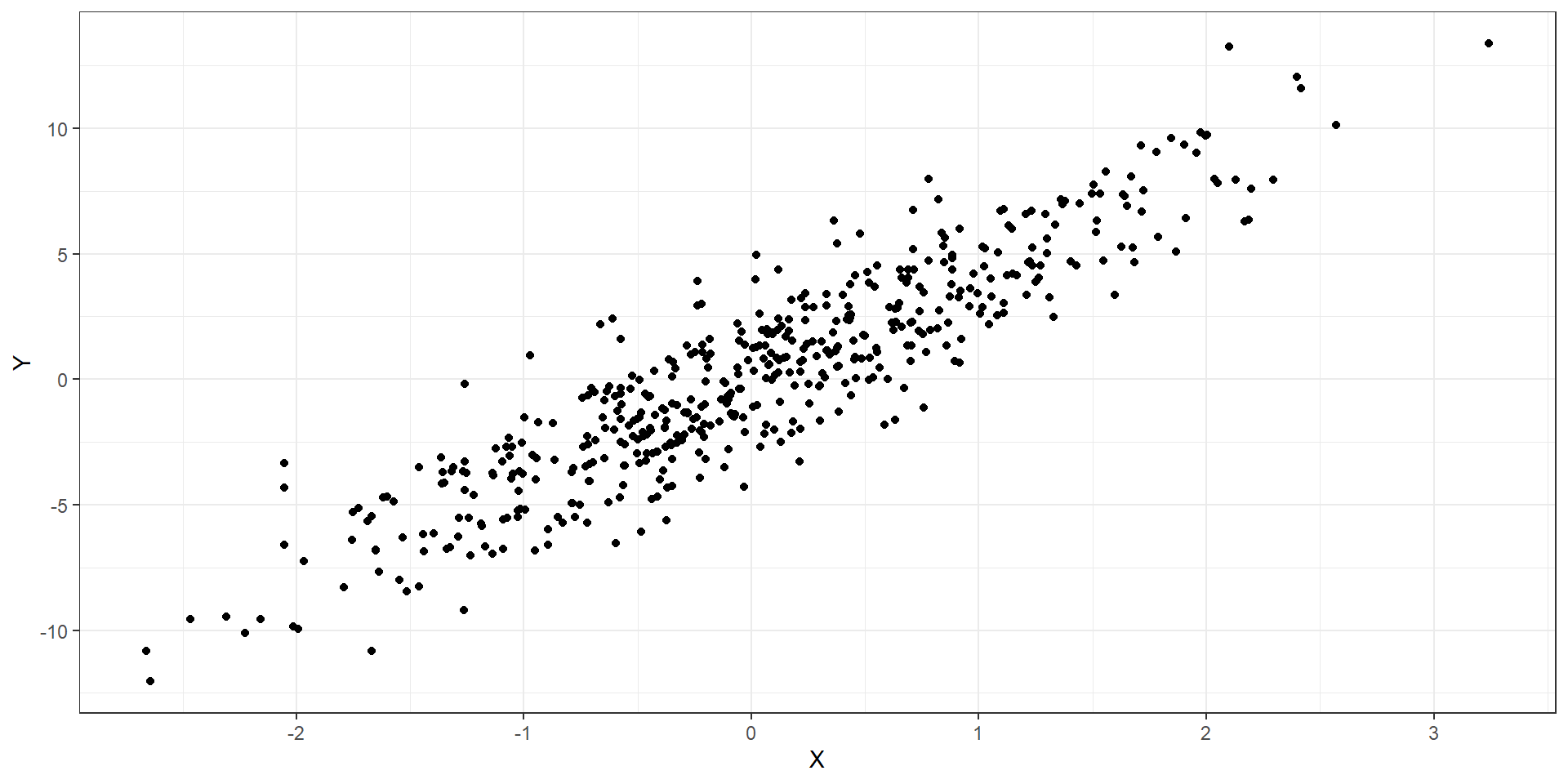
¿Cómo podemos resumir la relación entre ambas variables?

  • Podemos tratar de dibujar una línea recta que resuma la relación.

  • Existen infinitas rectas posibles que podríamos trazar: ¿Cuál elegir?

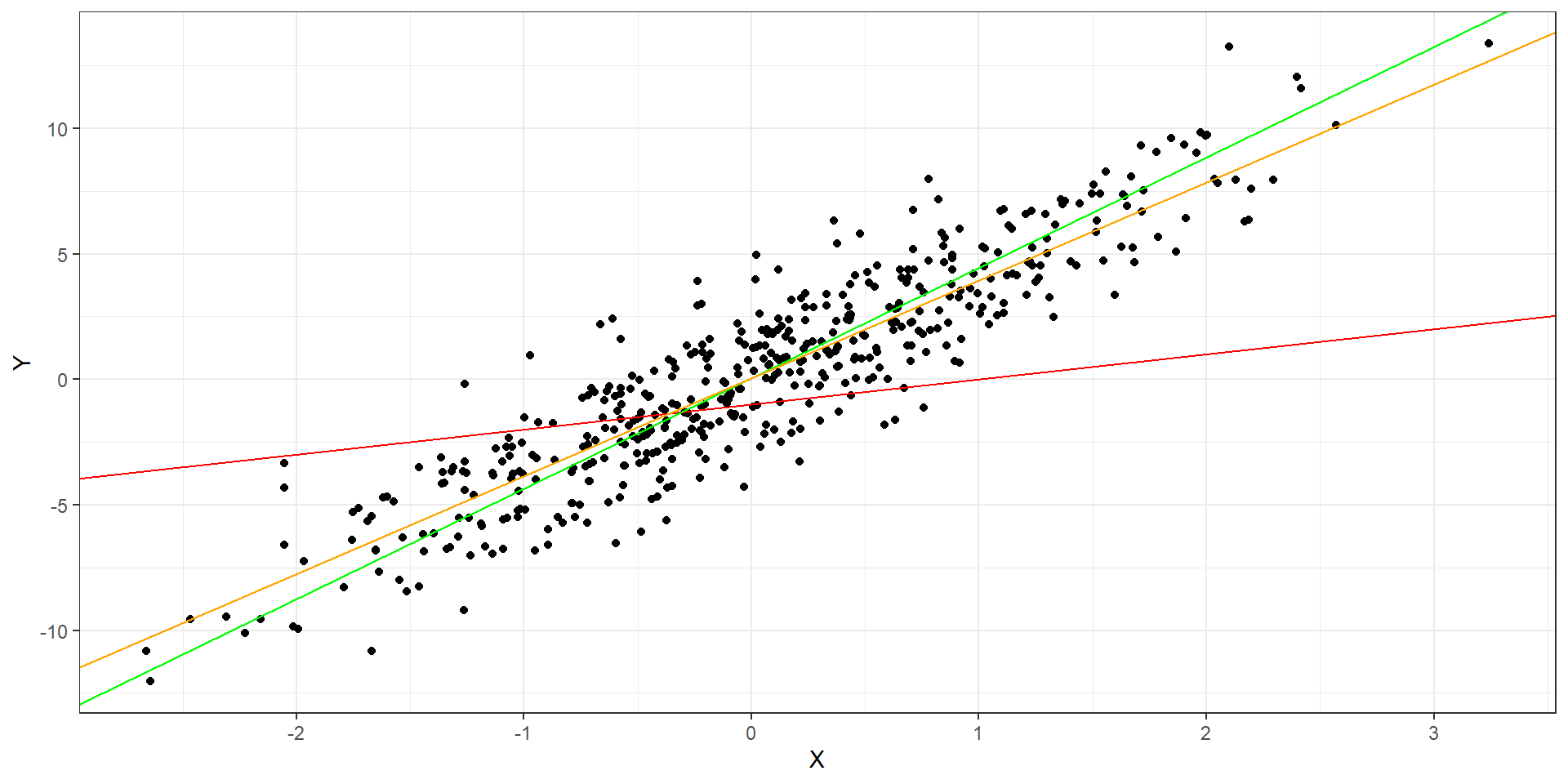
¿Cómo podemos resumir la relación entre ambas variables? (cont.)

  • Una opción sería elegir una recta que pase por el valor más representativo del yi en cada valor fijo de x1.
    • Una recta que conecte los promedios condicionados en x1

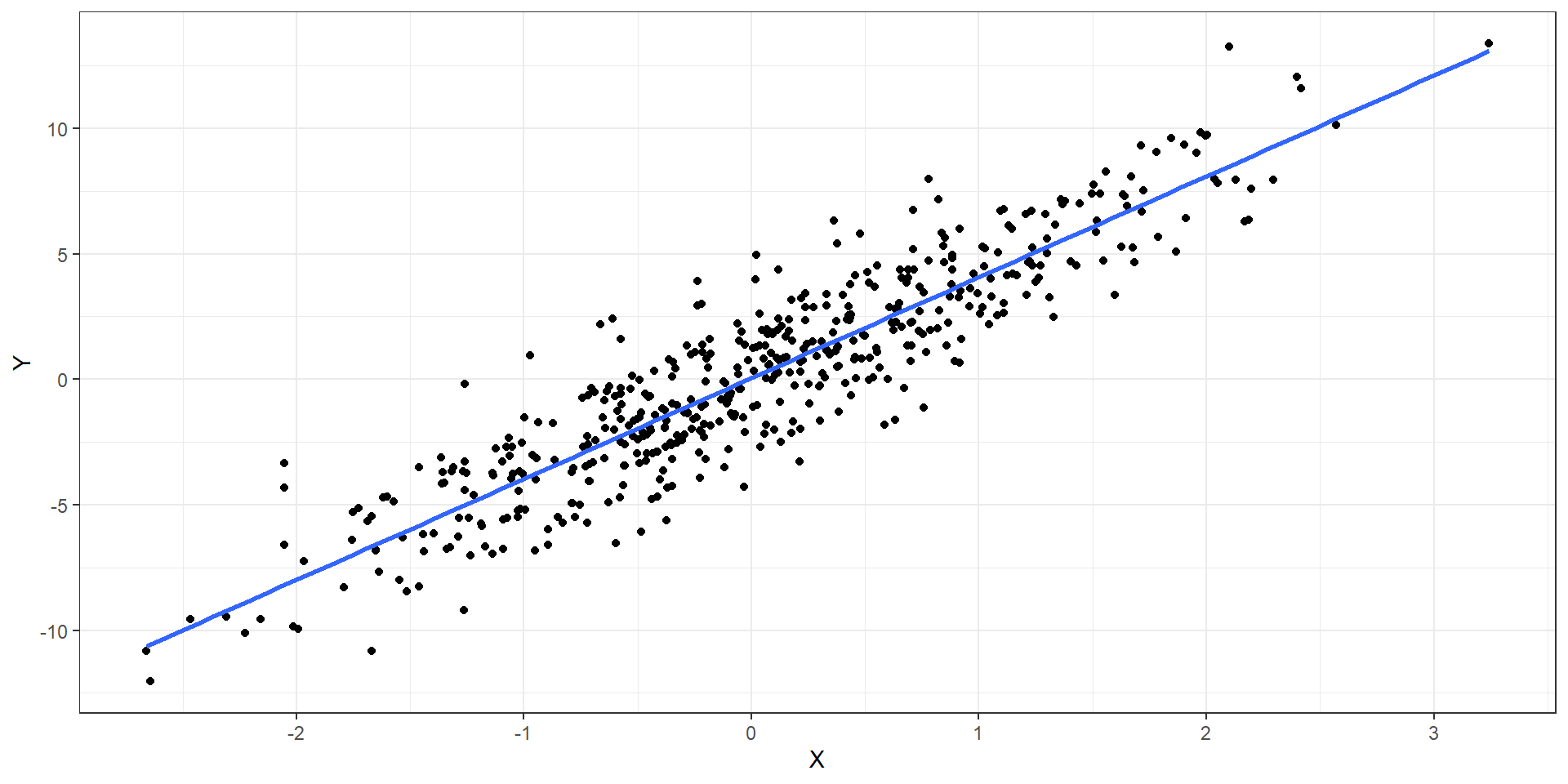
Anatomía de la RLS

  • Entonces, el modelo de regresión lineal simple se puede expresar de la siguiente manera:

yi=β0+β1x1i⏟componentesistemático+ϵi⏟componentealeatorio

  • El componente sistemático describe la media de yi en cada valor fijo de x1i: Media condicionada de y en x.

    • Pero el promedio no existe, los que existen son los individuos.

  • El componente aleatorio describe la variación de los individuos alrededor de cada media condiciona de y:

    • Se asume cierta distribución conocida.

Componente sistemático

  • Formalmente hablando, para cada observación i en la población, podemos relacionar el valor esperado (media) E[yi] de yi (también llamado μi) con la variable explicativa x1i mediante la siguiente ecuación lineal:

E[Y|X1=x1i]=E[yi]=μi=β0+β1x1i

  • Donde:
    • yi son realizaciones de variables aleatorias independientes e idénticamente distribuidas (i.i.d)
    • x1 es una variable cuyas valores son fijos y conocidos: x1i:
    • β0 y β1 son parámetros desconocidos de una superpoblación infinita.

Algunasn notas sobre el componente sistemático

x1 es fijo

  • Se asume se miden sin error.
  • No importa su distribución.

β0 y β1

  • Llamados coeficientes de regresión y son una medida de asociación.
  • Es lo que queremos estimar con los datos de la muestra!

Advertencia

  • Notar que el componente sistemático solo relaciona el promedio condicionado de yi con las variables explicativas, NO con los valores individuales.
  • Esta es una manera de obtener una medida que resuma las relaciones individuales en una sola medida.

Componente aleatorio

  • Para poder relacionar completamente los valores individuales con la ecuación de regersión se agrega un término de error ϵ, el cual se obtiene de restar el valor observado yi con el valor esperado de este (μi):

ϵi=yi−μi

  • El problema es que el término de error ϵi no puede predecirse ni estimarse con los datos, se considera que es el componente no explicado por la variable independiente.

    • Para lidiar con este, se asume que su comportamiento puede predecirse a nivel probabilístico: Se asume una distribución de este.
    • El error ϵi hereda la distribución de probabilidad de yi.

Componente aleatorio (cont.)

  • Por lo tanto, el valor individual de cada yi puede ser denotado por la siguiente expresión:

yi=β0+β1x1i+ϵi

  • Para hacer inferencia estadística, a menudo se asume lo siguiente:

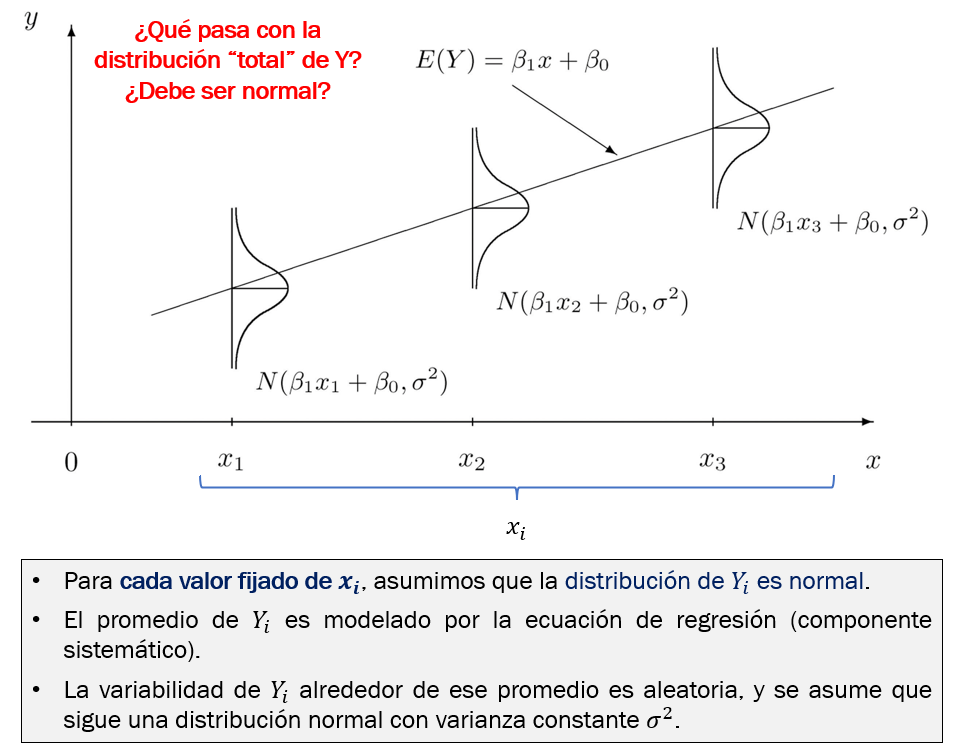
yi∼N(β0+β1x1i,σ2)

ϵi∼N(0,σ2)

En resumen

Estimación de ecuación de regresión

  • En la práctica no conocemos los valores de los parámetros, así que los estimamos de nuestros datos.

¿Cómo estimamos la ecuación lineal que mejor ajusta a los datos observados?

  • Usamos métodos numéricos:

    • Método de Mínimos Cuadrados Ordinarios (MCO)

    • Método de Máxima Verosimilitud (MV)

  • MCO y MV son equivalentes para el caso de la regresión lineal normal.

  • El estimador MCO es insesgado, no importa la distribución de yi o ϵi.

  • El estimador MCO tiene mínima varianza si y solo si:

    • Hay independencia de observaciones.
    • Hay normalidad.

Algunas notas sobre normalidad

  • No es necesario que ϵi o sigan una distribución normal para que los coeficientes de regresión β puedan estimarse de manera puntual.

  • Sin embargo, para estimar el valor p o los intervalos de confianza mediante inferencia clásica sí se necesita asumir una distribución conocida.

    • El modelo de regresión lineal normal asume normalidad de yi y ϵi.

    • Sin embargo, el modelo es robusto a desviaciones leves/moderadas de la normalidad cuando se cumple el TLC (número de observaciones grande).

  • Otros enfoques para inferencia flexibilizan este supuesto:

    • Bootstrap, varianza robusta, modelo lineal generalizado que asume otras distribuciones, etc.

Regresión Lineal Simple sobre variable explicativa categórica

  • Las variables categóricas no son continuas, en cambio son discretas y asumen solo unos cuantos valores.

  • ¿Cómo estimar una medida de asociación cuando la variable explicativa es categórica?

  • Veamos el caso binario.

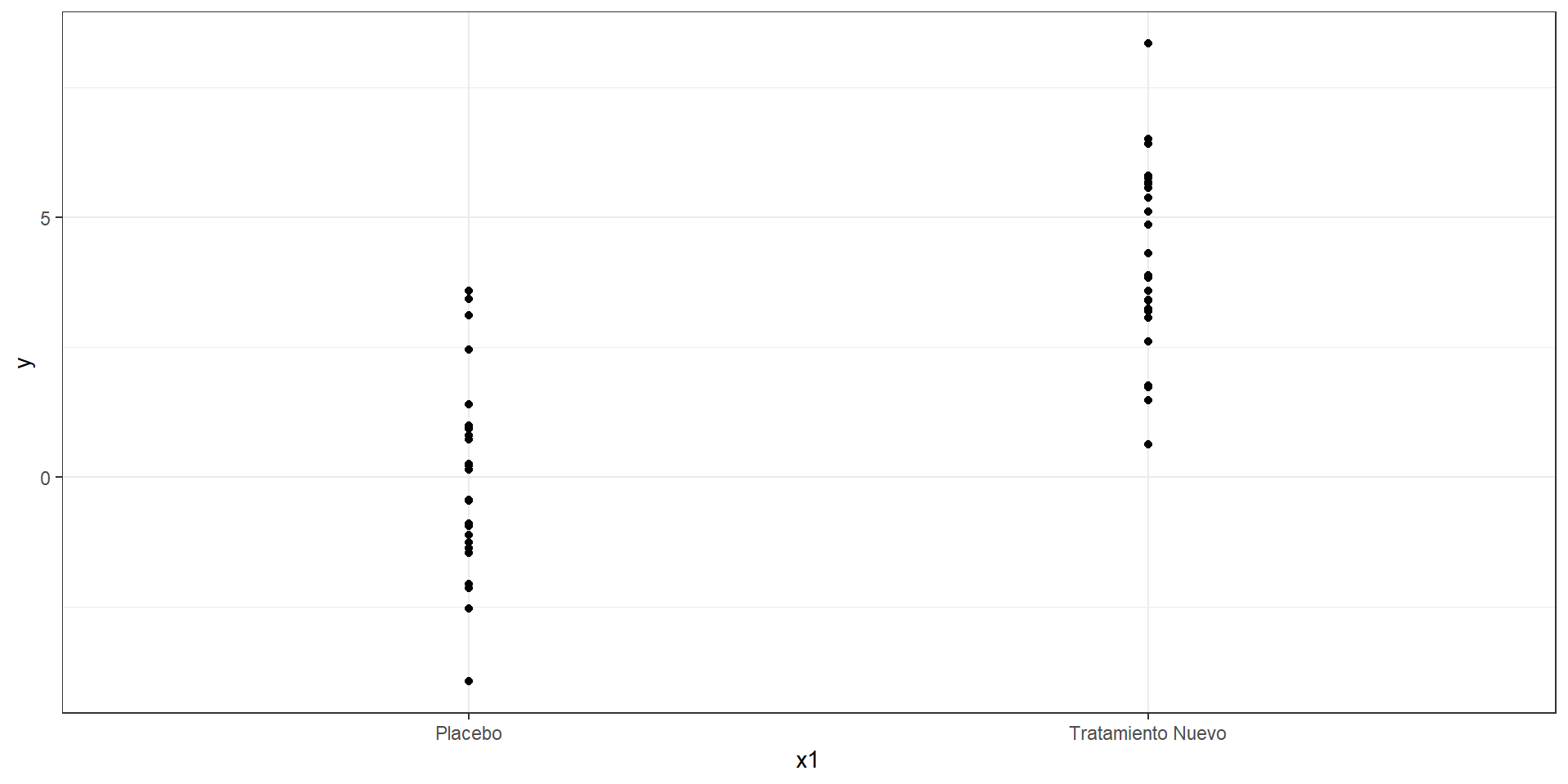
Regresión Lineal Simple sobre variable explicativa categórica (cont.)

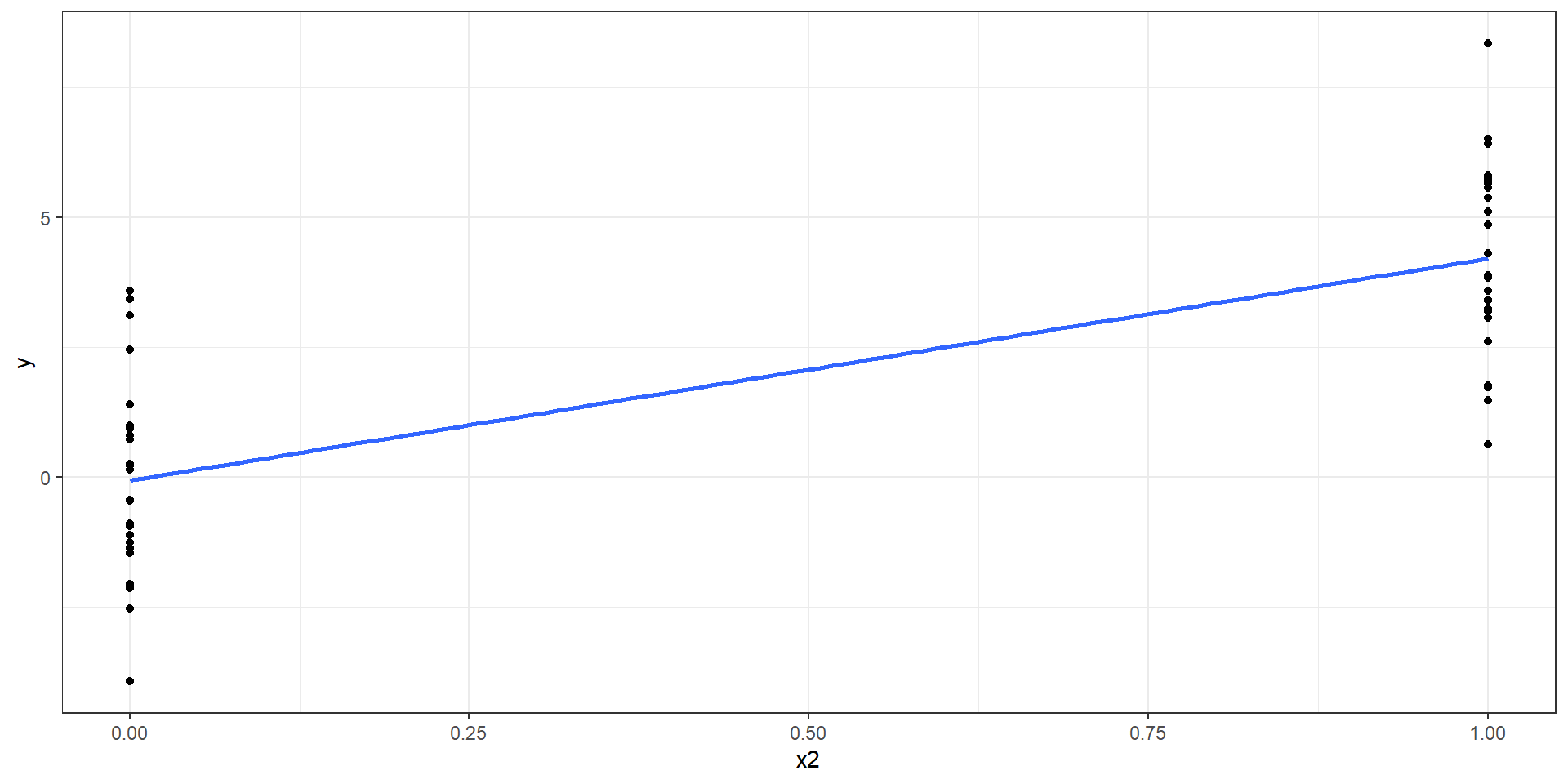
  • Si la variable es binaria, asignamos a una categoría el valor de 1 y a otra el valor de 0.

    • Asumiremos que la variable categórica es numérica para los efectos de todo cálculo.

    • Sin embargo, la interpretación se centrará en la comparación de categorías 0 y 1, nunca se interperará valores intermedios porquen o existen.

Regresión Lineal Simple en R

Agenda

  1. Introducción al modelado de regresión

  2. Modelo de Regresión Lineal Simple

  3. Regresión Lineal Simple en R

  4. Regresión Lineal Múltiple

  5. Regresión Lineal Múltiple en R

  6. Evaluación de Supuestos

lm() paso a paso

lm(y ~ x1, data = datos)

  • Se usa la función lm() de R base. Sin embargo, la salida de esta no es muy informativa:

    • Solo reportar coefiecientes de regresión (componente sistemático)

Call:
lm(formula = y ~ x1, data = datos)

Coefficients:
        (Intercept)  x1Tratamiento Nuevo  
           -0.06666              4.27094

lm() paso a paso

mod <- lm(y ~ x1, data = datos)

  • Se usa la función lm() de R base. Sin embargo, la salida de esta no es muy informativa:

  • El modelo puede guardarse para realizar más operaciones sobre este. Por ejemplo, mejorar la salida.

lm() paso a paso

mod <- lm(y ~ x1, data = datos)
summary(mod)

  • Se usa la función lm() de R base. Sin embargo, la salida de esta no es muy informativa:

  • El modelo puede guardarse para realizar más operaciones sobre este. Por ejemplo, mejorar la salida.

  • Podemos usar summary() para ver resultados detallados.


Call:
lm(formula = y ~ x1, data = datos)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.8666 -1.1168 -0.3487  1.3100  4.1336 

Coefficients:
                    Estimate Std. Error t value Pr(>|t|)    
(Intercept)         -0.06666    0.37316  -0.179    0.859    
x1Tratamiento Nuevo  4.27094    0.52773   8.093 1.59e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.866 on 48 degrees of freedom
Multiple R-squared:  0.5771,    Adjusted R-squared:  0.5683 
F-statistic:  65.5 on 1 and 48 DF,  p-value: 1.594e-10

Interpretación de salida de RLS

Regresión lineal simple con covariable numérica

  • lm()
  • Modelo estimado
  • Reporte tidy
  • Interpretación
  • Usamos la función lm():
mod <- lm(y_peso_final ~ x3_peso_inicial, data = datos2)
summary(mod)

Call:
lm(formula = y_peso_final ~ x3_peso_inicial, data = datos2)

Residuals:
     Min       1Q   Median       3Q      Max 
-10.0568  -4.7717  -0.8704   5.1824  10.4953 

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)      -5.4317     2.6574  -2.044   0.0412 *  
x3_peso_inicial   1.3447     0.1766   7.615  6.1e-14 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.535 on 998 degrees of freedom
Multiple R-squared:  0.05491,   Adjusted R-squared:  0.05397 
F-statistic: 57.99 on 1 and 998 DF,  p-value: 6.1e-14
  • El modelo estimado sería el siguiente:

y_pesofinal=−5.4317+1.3447∗x3_pesoinicial+ϵi

ϵi∼Normal(0,5.5352)

  • Usando el paquete {broom} y su función tidy() podemos obtener también los intervalos de confianza:
library(broom)
mod %>% 
  tidy(conf.int = TRUE) %>% 
  gt()
term estimate std.error statistic p.value conf.low conf.high
(Intercept) -5.431666 2.657423 -2.043960 4.121962e-02 -10.6464437 -0.2168874
x3_peso_inicial 1.344722 0.176587 7.615067 6.099526e-14 0.9981973 1.6912461

  • β0 o intercepto: Este viene a ser el valor promedio de y cuando todos los valores de x son 0. En este caso, cuando el peso inicial es cero kg. ¿Esto es posible?, por tal motivo, no se suele interpretar este valor.

  • β1 o coeficiente de regresión de x3_peso_inicial: Por cada 1 kg adicional de peso inicial, el valor promedio del peso final aumenta 1.43 kg (IC95% 1.00 a 1.69; p < 0.001).

Interpretación de salida de RLS

Regresión lineal simple con covariable categórica

  • lm()
  • Modelo estimado
  • Reporte tidy
  • Interpretación
  • Usamos la función lm():
mod <- lm(y_peso_final ~ x1_tto, data = datos2)
summary(mod)

Call:
lm(formula = y_peso_final ~ x1_tto, data = datos2)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.7043 -1.6644 -0.0095  1.5849  8.5658 

Coefficients:
                        Estimate Std. Error t value Pr(>|t|)    
(Intercept)              19.8771     0.1112  178.67   <2e-16 ***
x1_ttoTratamiento Nuevo -10.2325     0.1573  -65.04   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.488 on 998 degrees of freedom
Multiple R-squared:  0.8091,    Adjusted R-squared:  0.8089 
F-statistic:  4230 on 1 and 998 DF,  p-value: < 2.2e-16
  • El modelo estimado sería el siguiente:

y_pesofinal=19.8771−10.2325∗x3_ttoTratamientoNuevo+ϵi

ϵi∼Normal(0,2.4882)

  • Usando el paquete {broom} y su función tidy() podemos obtener también los intervalos de confianza:
mod %>% 
  tidy(conf.int = TRUE) %>% 
  gt()
term estimate std.error statistic p.value conf.low conf.high
(Intercept) 19.87711 0.1112478 178.67418 0 19.65880 20.095417
x1_ttoTratamiento Nuevo -10.23253 0.1573282 -65.03938 0 -10.54126 -9.923794

  • β0 (Intercept): A menudo no se interpreta. Es el valor promedio de yi cuando los valores de x son cero. En este caso, cuando el tratamien es cero (placebo). ¿Esto es posible?, sí es posible pero no es de ayuda para modelos explicativos, por lo que no se interpreta.

  • β1 x1Tratamiento Nuevo: El promedio de peso final en quienes recibieron el tratamiento nuevo fue 10.23 kg menor que el de quienes recibieron placebo (Dif. medias = -10.23; IC95% -10.54 a -9.92; p < 0.001).

Regresión Lineal Múltiple

Agenda

  1. Introducción al modelado de regresión

  2. Modelo de Regresión Lineal Simple

  3. Regresión Lineal Simple en R

  4. Regresión Lineal Múltiple

  5. Regresión Lineal Múltiple en R

  6. Evaluación de Supuestos

Regresión Lineal Múltiple

El modelo de regresión lineal múltiple generaliza la RLS permitiendo evaluar la relación de varias covariables explicativas x sobre yi.

  • Para p variables explicativas, el modelo puede expresarse como:

Componente sistemático:

E[Y|X1=x1i,...,Xp=xpi]=E[yi]=μi=β0+β1x1i+...+βpxpi

Componente aleatoria:

yi∼N(β0+β1x1i+...+βpxpi,Iσ2)

ϵi∼N(0,σ2)

Regresión Lineal en gráficos

  • RLS
  • RLM con 2 X
  • RLM con 3 o más X
  • La ecuación de la RLS representa una línea recta.

  • La ecuación de la RLM con dos variables explicativas ya no representa una línea recta, sino un plano recto.

  • Genera un hiperplano recto.

  • No podemos imaginarnos una imagen de esto, pero sí podemos analizarlo a nivel estadístico.

    • Algebra lineal proporciona herramientas para lidiar con esto usando matrices.

Regresión Lineal Múltiple en R

Agenda

  1. Introducción al modelado de regresión

  2. Modelo de Regresión Lineal Simple

  3. Regresión Lineal Simple en R

  4. Regresión Lineal Múltiple

  5. Regresión Lineal Múltiple en R

  6. Evaluación de Supuestos

lm() para RLM paso a paso

mod <- lm(y_peso_final ~ x1_tto, 
          data = datos2)
summary(mod)
  • El modelo RLS solo incluye una covariable.

Call:
lm(formula = y_peso_final ~ x1_tto, data = datos2)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.7043 -1.6644 -0.0095  1.5849  8.5658 

Coefficients:
                        Estimate Std. Error t value Pr(>|t|)    
(Intercept)              19.8771     0.1112  178.67   <2e-16 ***
x1_ttoTratamiento Nuevo -10.2325     0.1573  -65.04   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.488 on 998 degrees of freedom
Multiple R-squared:  0.8091,    Adjusted R-squared:  0.8089 
F-statistic:  4230 on 1 and 998 DF,  p-value: < 2.2e-16

lm() para RLM paso a paso

mod <- lm(y_peso_final ~ x1_tto + x3_peso_inicial, 
          data = datos2)
summary(mod)

  • El modelo RLS solo incluye una covariable.

  • El modelo de RLM incluye 2 o más covariables.

    • Estas se agregan con un símbolo +

    • Notar que no se reportan intervalos de confianza al 95%.


Call:
lm(formula = y_peso_final ~ x1_tto + x3_peso_inicial, data = datos2)

Residuals:
    Min      1Q  Median      3Q     Max 
-5.5598 -1.4213  0.1343  1.0768  5.4482 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept)              -0.94719    0.99689   -0.95    0.342    
x1_ttoTratamiento Nuevo -10.25530    0.13111  -78.22   <2e-16 ***
x3_peso_inicial           1.38755    0.06614   20.98   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.073 on 997 degrees of freedom
Multiple R-squared:  0.8676,    Adjusted R-squared:  0.8673 
F-statistic:  3266 on 2 and 997 DF,  p-value: < 2.2e-16

{broom} paso a paso

  • El paquete {broom} tiene funciones que facilitan obtener varios estadísticos de interés de los modelos de regresión.

  • La función tidy() permite obtener intervalos de confianza y otras medidas de interés.

{broom} paso a paso

  • El paquete {broom} tiene funciones que facilitan obtener varios estadísticos de interés de los modelos de regresión.

  • La función tidy() permite obtener intervalos de confianza y otras medidas de interés.

  • Además, retorna un tibble() que puede manipularse y luego embeberse en una tabla.

  • Primero se carga el paquete:

library(broom)

{broom} paso a paso

mod  %>% 
  tidy()
  • La función tidy() genera un resultado en formato tibble() que puede ser manipulado, exportado a excel, y convertido a tabla.
# A tibble: 3 × 5
  term                    estimate std.error statistic  p.value
  <chr>                      <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)               -0.947    0.997     -0.950 3.42e- 1
2 x1_ttoTratamiento Nuevo  -10.3      0.131    -78.2   0       
3 x3_peso_inicial            1.39     0.0661    21.0   3.10e-81

{broom} paso a paso

mod  %>% 
  tidy(conf.int = TRUE)
  • Con el argumento conf.int = TRUE mostramos también los intervalos de confianza.
# A tibble: 3 × 7
  term                    estimate std.error statistic  p.value conf.low conf.…¹
  <chr>                      <dbl>     <dbl>     <dbl>    <dbl>    <dbl>   <dbl>
1 (Intercept)               -0.947    0.997     -0.950 3.42e- 1    -2.90    1.01
2 x1_ttoTratamiento Nuevo  -10.3      0.131    -78.2   0          -10.5   -10.0 
3 x3_peso_inicial            1.39     0.0661    21.0   3.10e-81     1.26    1.52
# … with abbreviated variable name ¹​conf.high

{broom} paso a paso

mod  %>% 
  tidy(conf.int = TRUE) %>% 
  gt()
  • Podemos convertir en tabla gt() para mejorar visualización
term estimate std.error statistic p.value conf.low conf.high
(Intercept) -0.9471917 0.99689433 -0.9501426 3.422701e-01 -2.903444 1.009060
x1_ttoTratamiento Nuevo -10.2553009 0.13110928 -78.2194924 0.000000e+00 -10.512583 -9.998019
x3_peso_inicial 1.3875541 0.06613671 20.9800905 3.097784e-81 1.257771 1.517337

{broom} paso a paso

mod  %>% 
  tidy(conf.int = TRUE) %>% 
  rio::export("tabla_regresion.xlsx")
  • Otra opción es decargar los resultados en un excel, con la función export() del paquete {rio}

{broom} paso a paso

mod  %>% 
  tidy(conf.int = TRUE) %>% 
  mutate(estimate = round(estimate, 2), 
         conf.low = round(conf.low, 2), 
         conf.high = round(conf.high, 2), 
         p.value2 = case_when(
           p.value < 0.001 ~ "<0.001", 
           p.value >= 0.001 ~ as.character(round(p.value, 3))
         )) %>% 
  select(term, estimate, conf.low, conf.high, p.value2) %>% 
  gt()
term estimate conf.low conf.high p.value2
(Intercept) -0.95 -2.90 1.01 0.342
x1_ttoTratamiento Nuevo -10.26 -10.51 -10.00 <0.001
x3_peso_inicial 1.39 1.26 1.52 <0.001
  • También podemos manipular la tabla para personalizarla usando “verbos” del paquete {dplyr}.

{broom} paso a paso

mod  %>% 
  tidy(conf.int = TRUE) %>% 
  mutate(estimate = round(estimate, 2), 
         conf.low = round(conf.low, 2), 
         conf.high = round(conf.high, 2), 
         p.value2 = case_when(
           p.value < 0.001 ~ "<0.001", 
           p.value >= 0.001 ~ paste("= ", round(p.value, 3))
         )) %>% 
  mutate(
    `Coeficiente (IC95%), p valor` = 
      glue("{estimate} (IC95% {conf.low} a {conf.high}), p {p.value2}"), 
    Variables = c("Intercepto", "Tratamiento nuevo vs. Placebo", "Peso inicial (kg)")
  ) %>% 
  select(Variables, `Coeficiente (IC95%), p valor`) %>% 
  gt()
Variables Coeficiente (IC95%), p valor
Intercepto -0.95 (IC95% -2.9 a 1.01), p = 0.342
Tratamiento nuevo vs. Placebo -10.26 (IC95% -10.51 a -10), p <0.001
Peso inicial (kg) 1.39 (IC95% 1.26 a 1.52), p <0.001
  • Incluso más personalización de lo que imaginan…

En resumen

  • Modelo estimado
  • Modelo para interpretación
  • Interpretación
mod <- lm(y_peso_final ~ x1_tto + x3_peso_inicial, data = datos2)
summary(mod)

Call:
lm(formula = y_peso_final ~ x1_tto + x3_peso_inicial, data = datos2)

Residuals:
    Min      1Q  Median      3Q     Max 
-5.5598 -1.4213  0.1343  1.0768  5.4482 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept)              -0.94719    0.99689   -0.95    0.342    
x1_ttoTratamiento Nuevo -10.25530    0.13111  -78.22   <2e-16 ***
x3_peso_inicial           1.38755    0.06614   20.98   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.073 on 997 degrees of freedom
Multiple R-squared:  0.8676,    Adjusted R-squared:  0.8673 
F-statistic:  3266 on 2 and 997 DF,  p-value: < 2.2e-16

y_pesofinal=−0.94719−10.25530∗x1ttoTratamientoNuevo+1.3875∗x3_pesoinicial+ϵi

ϵi∼Normal(0,2.0732)

term estimate std.error statistic p.value conf.low conf.high
(Intercept) -0.9471917 0.99689433 -0.9501426 3.422701e-01 -2.903444 1.009060
x1_ttoTratamiento Nuevo -10.2553009 0.13110928 -78.2194924 0.000000e+00 -10.512583 -9.998019
x3_peso_inicial 1.3875541 0.06613671 20.9800905 3.097784e-81 1.257771 1.517337
 
mod <- lm(y_peso_final ~ x1_tto + x3_peso_inicial, data = datos2)

mod %>% 
  tidy(conf.int = TRUE) %>% 
  gt()

  • β0 o intercepto: Este viene a ser el valor promedio de y cuando todos los valores de x son 0. En este caso, cuando el peso inicial es cero kg y cuando el tratamiento es placebo. ¿Esto es posible?, por tal motivo, no se suele interpretar este valor.

  • β2 o coeficiente de regresión de x1_ttoTratamiento Nuevo: El promedio de peso final en quienes recibieron el tratamiento nuevo fue 10.26 kg menor que el de quienes recibieron placebo, luego de ajustar por peso inicial (Dif. medias = -10.26; IC95% -10.51 a -9.99; p < 0.001).

  • β1 o coeficiente de regresión de x3_peso_inicial: Por cada 1 kg adicional de peso inicial, el valor promedio del peso final aumenta 1.39 kg, luego de ajustar por tatamiento recibido (IC95% 1.26 a 1.52; p < 0.001).

Evaluación de Supuestos

Agenda

  1. Introducción al modelado de regresión

  2. Modelo de Regresión Lineal Simple

  3. Regresión Lineal Simple en R

  4. Regresión Lineal Múltiple

  5. Regresión Lineal Múltiple en R

  6. Evaluación de Supuestos

Errores y residuos

  • Los errores (ϵi) son medidas de la población a la que no tenemos acceso.

    • Sin embargo, varios supuestos de la regresión involucran a los errores inaccesibles por el investigador.

  • Los residuos (ei) son el análogo a los errores pero obtenidos de la muestra observada.

  • Podemos usar los residuos para evaluar algunos supuestos sobre los errores.

Residuos gráficamente

Supuestos de la regresión lineal normal

Supuestos estadísticos del modelo

  • Linealidad

  • Independencia de observaciones

  • Homocedasticidad de los errores ϵi

  • Normalidad de los errores ϵi o de yi.

  • No problemas con la regresión:

    • Puntos influyentes.
    • (Multi) colinealidad: Solo cuando es un problema, no siempre lo es.

Supuestos adicionales que suelen acompañar a la regresión lineal normal

  • Generalizar a población finita conocida
  • Inferencia causal

Supuestos si queremos generalizar a una población finita bien definida

  • La muestra es representativa de la población.

    • Ideal para alcanzar esto es mediante muestreo probabilístico: representatividad estadística.

  • Cuando no lo tenemos, solo podemos generalizar a una población que sabemos que existe pero no podemos definir. ¿Qué tan relevante puede ser esto?

    • Otros consideran (¿ingenuamente?) que, bajo ciertas condiciones, se puede alcanar una representativadad teórica.

  • Hay asignación aleatoria

    • Ideal para alcanzar esto es mediante experimento aleatorizado.

  • Cuando no lo tenemos, tenemos que poder asumir (¿ingenuamente?) que se puede emular la asignación aleatoria de alguna manera:

    • El ajuste de regresión por confusores es una manera de pensar en esto.

Algunas notas sobre los errores y residuos para evaluar supuestos

  • En realidad, los supuestos de los modelos lineales son sobre el comportamiento probabilístico de yi.

  • Sin embargo, la idea de la existencia de los errores y de sus valores observados en la muestra, residuos resulta útil para evaluar supuestos.

    • Permiten reducir un problema de muchas dimensiones a solo 1 o 2 dimensiones.

    • Son como las placas radiográficas para el diagnóstico de los modelos.

Algunas notas sobre los errores y residuos para evaluar supuestos

¿Cómo evaluar los supuestos de la regresión lineal?

  • Se usan los residuos para explorar el comportamiento de los yi o los errores ϵ.

  • Preferiblemente usar gráficos de residuos.

    • Pruebas de hipótesis que usan residuos tienen los mismos problemas que discutimos en clases anteriores.

    • Podríamos usarlas para complementar análisis cuando los tamaños de muestra no son ni muy pequeños ni muy grandes.

  • La función check_model del paquete {performance} genera un panel de gráficos muy útil para evalur estos supuestos.

  • Podemos complentar el análisis de supuestos con funciones del paquete {car}.

Función check_model() para evaluar supuestos

  • Podemos observar un panel general con la evaluación de varios supuestos

  • Primero cargamos el paquete performance:

library(performance)

  • Luego, la función check_model() aplicada al objeto de modelado genera un panel de gráficos para evaluar diversos supuestos o detectar algunos problemas.

  • Los gráficos de homogeneidad de varianzas, linealidad y de normalidad de residuos usan residuos estandarizados para el caso de lm()

check_model(mod)

Función check_model() para evaluar supuestos (cont.)

Linealidad

  • La función check_model() genera un gráfico de residuos versus valores ajustados que permiten evaluar linealidad.

  • Podemos graficar los residuos contra cada variable predictora numérica para identificar si alguna de estas variables es causante de no linealidad e incluso tener una idea de qué forma funcional podría ser apropiada.

  • Los gráficos de residuos crudos, los estandarizados, e incluso los estudentizdos versus cada covariable pueden no generar gráficos donde se visualicen apropiadamente la no linealidad.

  • Los residuos parciales son un tipo de residuo que genera gráficos de mejor “resolución” para diagnosticar problemas de no linealidad.

Linealidad con el paquete {car}

  • Podemos usar gráficos de residuos parciales + Componente:
library(car)
crPlots(mod)

Linealidad con el paquete {car} (cont.)

  • También podemos usar gráficos de variable agregada
avPlots(mod)

Linealidad con función termplot() de paquete {stats} (cont.)

termplot(mod, partial.resid = TRUE, se = TRUE, ask = FALSE, smooth = panel.smooth)

Linealidad con el paquete {ggeffects} (cont.)

library(ggeffects)
xb <- ggpredict(mod, "x3_peso_inicial [all]")
plot(xb, residuals = TRUE, residuals.line = TRUE)

Homogeneidad de varianzas (Homocedasticidad)

  • Se puede evaluar si la homocedasticidad es consistente según cada variable predictora.

  • Se sugiere usar residuos estudentizados.

residualPlots(mod, type = "rstudent")
                Test stat Pr(>|Test stat|)
x1_tto                                    
x3_peso_inicial    1.2180           0.2235
Tukey test         0.5429           0.5872

Homogeneidad de varianzas (Homocedasticidad)

residualPlots(mod, type = "rstudent")
                Test stat Pr(>|Test stat|)
x1_tto                                    
x3_peso_inicial    1.2180           0.2235
Tukey test         0.5429           0.5872

Outliers, puntos influyentes y dfbetas

  • Diversas medidas pueden usarse para detectar la existencia de valores extremos y puntos de alto apalancamiento que puedan ser influyentes.

  • La función influenceIndexPlot() del paquete {car} es muy útil para generar estos gráficos.

influenceIndexPlot(model = mod, id.n = 5)

Outliers, puntos influyentes y dfbetas

influenceIndexPlot(model = mod, id.n = 5)

Outliers, puntos influyentes y dfbetas

  • En el caso de modelos explicativos, importa determinar si hay un impacto en los coeficientes de regresion.

  • Los dfbetas pueden ser útiles para evaluar esto:

dfbetasPlots(model = mod, id.n = 5)

¿Cómo flexibilizar supuestos?

  • No linealidad
  • Forma funcional
  • NUNCA categorice

  • El supuesto de linealidad es sobre los coeficientes de regresión β, no sobre las covariables.

  • Las variables X deben estar en una forma apropiada para que el supuesto se cumpla.

  • Es bien difícil que exista linealidad en la realidad, pero puede ocurrir en raras y excepcionales ocasiones.

    • Sobre todo cuando la variable está acotada en valores donde la linealidad es plausible.

  • Se sugiere asumir no linealidad y pre-planear un modelamiento no lineal de la forma funcional de los predictores.

  • Entre los métodos que pueden usarse, tenemos:

    • Splines: Bastante usado y sugerido en bioestadística. Útil para ajustar por variables continuas.

    • Modelamiento Multivariablede polinomios fraccionales. También usado y recomendado en literatura biomédica. Útil para modelar forma como objetivo principal.

    • Polinomios. Menos flexible, puede ser útil si se conoce bien la relación o se busca mejorar ajuste.

    • Modelos aditivos generalizados. Útil si se buscar modelar la relación. Complejos y requieren muchos datos.

Evite categorizar la variable continua

  • Categorizar es muy malo: se pierde información y se corre el riesgo de sesgar resultados.

  • Si se quiere ajustar por variables continuas, use Splines o Polinomios fraccionales. No requiere interpretar sus resultados, pero si ajsutar bien!

  • Si se quiere evaluar la relación de la variable continua, planee un método estadístico para modelar la forma sin asumir linealidad.

    • Presuponga que la relación no es lineal.

    • Modelo y responda su pregunta. Si la relación es lineal, el modelo más complejo revelerá una línea recta.

¿Cómo flexibilizar supuestos? (cont.)

  • Heterocedasticidad
  • No normalidad

  • No homogeneidad de varianzas: Podemos usar una estimación robusta de la varianza o modelar directamente la varianza.

  • Los paquetes {sanwich} y {lmtest} proporcionan funciones útiles para estimación robusta de varianza.

  • Es bien difícil de creer que existe homogeneidad de varianzas en la vida real (salvo muy raras y excepcionales ocasiones).

    • Se sugiere planear el proyecto asumiendo que no hay homocedasticidad y usar inferencia robusta de manera pre-planeada.
library(lmtest)
library(sandwich)
coeftest(mod, vcov = vcovHC) %>% 
  tidy(conf.int = TRUE)
# A tibble: 3 × 7
  term                    estimate std.error statistic  p.value conf.low conf.…¹
  <chr>                      <dbl>     <dbl>     <dbl>    <dbl>    <dbl>   <dbl>
1 (Intercept)               -0.947    1.05      -0.906 3.65e- 1    -3.00    1.10
2 x1_ttoTratamiento Nuevo  -10.3      0.131    -78.1   0          -10.5   -10.0 
3 x3_peso_inicial            1.39     0.0692    20.0   2.45e-75     1.25    1.52
# … with abbreviated variable name ¹​conf.high

  • Si distribución es normal (cosa que no podemos saber con certeza), podemos dejar de preocuparnos por este supuesto.

  • Si se cumple TLC, podemos dejar de preocuparnos por este supuesto.

  • Si no se cumple TLC o hay dudas razonables, podemos optar por alguna de las siguientes alternativas:

    • Transformar Y para normalizar (p. ej., logaritmo)
    • Usar varianza robusta
    • Estimar varianza con bootstrapping u otro método de remuestreo.

¡Gracias!
¿Preguntas?




https://github.com/psotob91

percys1991@gmail.com

R Aplicado a los Proyectos de Investigación - Sesión 8

1 / 69
Sesión 8 Curso: R Aplicado a los Proyectos de Investigación Percy Soto-Becerra, M.D., M.Sc(c) InkaStats Data Science Solutions | Medical Branch 2022-10-19 https://github.com/psotob91

  1. Slides

  2. Tools

  3. Close
  • Sesión 8
  • Introducción al modelado de regresión
  • Análisis de regresión
  • Modelos de regresión multivariable
  • ¿Para qué usamos los modelos de regresión?
  • Propósitos del modelamiento
  • Propósitos del modelamiento (cont.)
  • ¿Para qué usamos los modelos de regresión? (cont.)
  • Modelo de Regresión Lineal Simple
  • Regresión Lineal
  • Relación entre dos variables
  • ¿Cómo podemos resumir la relación entre ambas variables?
  • ¿Cómo podemos resumir la relación entre ambas variables? (cont.)
  • Anatomía de la RLS
  • Componente sistemático
  • Algunasn notas sobre el componente sistemático
  • Componente aleatorio
  • Componente aleatorio (cont.)
  • En resumen
  • Estimación de ecuación de regresión
  • ¿Cómo estimamos la ecuación lineal que mejor ajusta a los datos observados?
  • Algunas notas sobre normalidad
  • Regresión Lineal Simple sobre variable explicativa categórica
  • Regresión Lineal Simple sobre variable explicativa categórica (cont.)
  • Regresión Lineal Simple en R
  • lm() paso a paso
  • lm() paso a paso
  • lm() paso a paso
  • Interpretación de salida de RLS
  • Interpretación de salida de RLS
  • Regresión Lineal Múltiple
  • Regresión Lineal Múltiple
  • Regresión Lineal en gráficos
  • Regresión Lineal Múltiple en R
  • lm() para RLM paso a paso
  • lm() para RLM paso a paso
  • {broom} paso a paso
  • {broom} paso a paso
  • {broom} paso a paso
  • {broom} paso a paso
  • {broom} paso a paso
  • {broom} paso a paso
  • {broom} paso a paso
  • {broom} paso a paso
  • En resumen
  • Evaluación de Supuestos
  • Errores y residuos
  • Residuos gráficamente
  • Supuestos de la regresión lineal normal
  • Supuestos adicionales que suelen acompañar a la regresión lineal normal
  • Algunas notas sobre los errores y residuos para evaluar supuestos
  • Algunas notas sobre los errores y residuos para evaluar supuestos
  • ¿Cómo evaluar los supuestos de la regresión lineal?
  • Función check_model() para evaluar supuestos
  • Función check_model() para evaluar supuestos (cont.)
  • Linealidad
  • Linealidad con el paquete {car}
  • Linealidad con el paquete {car} (cont.)
  • Linealidad con función termplot() de paquete {stats} (cont.)
  • Linealidad con el paquete {ggeffects} (cont.)
  • Homogeneidad de varianzas (Homocedasticidad)
  • Homogeneidad de varianzas (Homocedasticidad)
  • Outliers, puntos influyentes y dfbetas
  • Outliers, puntos influyentes y dfbetas
  • Outliers, puntos influyentes y dfbetas
  • ¿Cómo flexibilizar supuestos?
  • ¿Cómo flexibilizar supuestos? (cont.)
  • ¡Gracias! ¿Preguntas?...
  • https://github.com/psotob91...
  • f Fullscreen
  • s Speaker View
  • o Slide Overview
  • e PDF Export Mode
  • b Toggle Chalkboard
  • c Toggle Notes Canvas
  • d Download Drawings
  • ? Keyboard Help