Sesión 9

Curso: R Aplicado a los Proyectos de Investigación

Percy Soto-Becerra, M.D., M.Sc(c)

InkaStats Data Science Solutions | Medical Branch

2022-10-21

  https://github.com/psotob91

El Modelo Lineal Generalizado

Agenda

  1. El Modelo Lineal Generalizado

  2. La regresión de Poisson

  3. La regresión Binomial Negativa

  4. Tablas de regresión reproducibles con {gtsummary}

Modelo Lineal Generalizado

Modelo lineal que permite modelar desenlaces de varios tipos de distribuciones.

  • Generaliza el modelo de regresión lineal.

  • Permite que Yi siga otras distribuciones.

    • Pertenecientes a la familia de distribución exponencial.

Modelo Lineal Generalizado: Anatomía

Componente sistemático:

g(E(Y|x1i,...,xpi))=g(E(Yi))=ηi=β0+β1x1i+...+βpxip

  • g() es la función de enlace.

  • ηi es el predictor linear.

  • E(Y|x1i,...,xpi)=μi

Componente aleatorio:

Yi∼Distribucion de la Familia Exponencial

Familia exponencial

Variable respuesta Distribución de FE Función de enlace canónica g() Otras funciones de enlace comunes
Binaria Bernoulli (Binomial con n = 1) logit() log()
Conteo Binomial (con n > 1) logit() log()
Poisson log()
Binomial negativo log(μ+k) log()
Continua positiva Gamma 1μ
Gausiana inversa

Estimación de GLM

  • Hace uso de estimación de máxima verosimilitud (MV).

  • Salvo el caso normal (donde MV = MCO), no existe solución cerrada para obtener los estimadores de MV.

    • Hay que hacer uso de métodos numéricos: Fisher Scoring, Newton Raphson, etc.

  • No siempre la función de verosimilitud tiene un máximo.

    • Solo cuando se usa la función de enlace canónica.

    • Caso contrario, puede no tener solución única y hay problemas de convergencia.

La regresión de Poisson

Agenda

  1. El Modelo Lineal Generalizado

  2. La regresión de Poisson

  3. La regresión Binomial Negativa

  4. Tablas de regresión reproducibles con {gtsummary}

El modelo de regresión de Poisson

yi∼Poisson(β0+β1x1i+...+βpxip)

  • Componente sistemático:

log(E(yi))=ηi

  • Función de enlace:

ηi=β0+β1x1i+...+βpxip

  • Componente aleatorio:

yi∼Poisson(ηi)

¿Por qué usar log?

  • log() es la función de enlace canónica: solución única para MV y no problemas de convergencia por esto.

  • Si usamos la función identidad de la regresión lineal, el modelo quedaría planetado de esta manera:

E(yi)=β0+β1x1i+...+βpxip

  • Entonces, el modelo predecirá valores fuera del rango natural de la variable yi:
  • yi es de conteo (discreto), pero se obtendrían predichos con decimales (continuo).
  • yi es positivo siempre, pero se podrían ontener predichos negativos.
  • El inverso de log(), exp() devuelve una razón de medias, medida interpretable.

¿Por qué no asumir normalidad de yi?

  • Porque la distribución de yi no es normal, es una variable de conteo.

  • El principal problema de esto, es que al ser Poisson, la media=varianza=λ, por lo que a mayor valor de la media, la varianza aumentará.

    • Lo que implica que yi es una v.a. heterocedástica.

    • El modelo normal necesita homocedasticidad, caso contrario, tiene que corregirse de alguna manera.

    • Poisson no necesita esto, su modelo es heterocedastico por naturaleza, lo que hace más eficiente la estimación:

      • Si el modelo es válido, los intervalos de confianza serán más precisos.

La regresión de Poisson retorna razón de medias

  • La regresión de Poisson permite retornar directamente razón de medias (RM).

  • Los coeficientes de regresión β del modelo son log(RM), por lo tanto, podemos exponenciarlos para obtener los OR:

β=log(RM)

entonces

eβ=RM

glm() paso a paso

mod <- glm(docvis ~ female + age, 
           data = md_visit)
summary(mod)

Call:
glm(formula = docvis ~ female + age, data = md_visit)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
 -5.139   -2.792   -1.623    0.593  118.711  

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.442309   0.168002  -2.633  0.00848 ** 
female       0.980325   0.082751  11.847  < 2e-16 ***
age          0.071883   0.003682  19.522  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for gaussian family taken to be 33.29453)

    Null deviance: 671518  on 19608  degrees of freedom
Residual deviance: 652772  on 19606  degrees of freedom
AIC: 124390

Number of Fisher Scoring iterations: 2

  • Se especifica la ecuación.

    • Por defecto, regresión lineal normal

glm() paso a paso

mod <- glm(docvis ~ female + age, 
           family = poisson, 
           data = md_visit)
summary(mod)

Call:
glm(formula = docvis ~ female + age, family = poisson, data = md_visit)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-3.3562  -2.2285  -1.1346   0.3396  26.8860  

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -0.0368083  0.0176597  -2.084   0.0371 *  
female       0.3092910  0.0081168  38.105   <2e-16 ***
age          0.0227500  0.0003624  62.768   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 122270  on 19608  degrees of freedom
Residual deviance: 116363  on 19606  degrees of freedom
AIC: 153636

Number of Fisher Scoring iterations: 6

  • Se indica la familia de distribución de yi.

    • Por defecto, la función de enlace será la canónica.

glm() paso a paso

mod <- glm(docvis ~ female + age, 
           family = poisson(link = "log"), 
           data = md_visit)
summary(mod)

Call:
glm(formula = docvis ~ female + age, family = poisson(link = "log"), 
    data = md_visit)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-3.3562  -2.2285  -1.1346   0.3396  26.8860  

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -0.0368083  0.0176597  -2.084   0.0371 *  
female       0.3092910  0.0081168  38.105   <2e-16 ***
age          0.0227500  0.0003624  62.768   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 122270  on 19608  degrees of freedom
Residual deviance: 116363  on 19606  degrees of freedom
AIC: 153636

Number of Fisher Scoring iterations: 6

  • Se indica la familia de distribución de yi.

    • Por defecto, la función de enlace será la canónica.

glm() paso a paso

mod <- glm(docvis ~ female + age, 
           family = poisson(link = "identity"), 
           data = md_visit)
summary(mod)

Call:
glm(formula = docvis ~ female + age, family = poisson(link = "identity"), 
    data = md_visit)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-3.1714  -2.2486  -1.1320   0.3312  26.8394  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -0.18852    0.04629  -4.073 4.64e-05 ***
female       1.00553    0.02510  40.056  < 2e-16 ***
age          0.06581    0.00110  59.848  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 122270  on 19608  degrees of freedom
Residual deviance: 116471  on 19606  degrees of freedom
AIC: 153743

Number of Fisher Scoring iterations: 6
  • Podemos cambiar la función de enlace.

glm() paso a paso

mod <- glm(docvis ~ female + age, 
           family = poisson(link = "log"), 
           data = md_visit)
mod %>% 
  tidy() %>% 
  gt()
term estimate std.error statistic p.value
(Intercept) -0.03680829 0.0176596601 -2.084315 0.03713153
female 0.30929097 0.0081167612 38.105220 0.00000000
age 0.02275001 0.0003624464 62.767938 0.00000000
  • En el caso de la función de enlace log, los coeficientes son log(razón de medias), para volverlos interpretables, hay que aplicar antilogaritmo: exp().

glm() paso a paso

mod %>% 
  tidy(exponentiate = TRUE) %>% 
  gt()
term estimate std.error statistic p.value
(Intercept) 0.9638609 0.0176596601 -2.084315 0.03713153
female 1.3624587 0.0081167612 38.105220 0.00000000
age 1.0230108 0.0003624464 62.767938 0.00000000
  • La función tidy() de {broom} permite hacer esto facilmente: exponentiate = TRUE.

glm() paso a paso

mod %>% 
  tidy(exponentiate = TRUE, conf.int = TRUE) %>% 
  gt()
term estimate std.error statistic p.value conf.low conf.high
(Intercept) 0.9638609 0.0176596601 -2.084315 0.03713153 0.9310334 0.9977672
female 1.3624587 0.0081167612 38.105220 0.00000000 1.3409630 1.3843148
age 1.0230108 0.0003624464 62.767938 0.00000000 1.0222845 1.0237380
  • También podemos agregar intervalos de confianza.

Casos aplicado

  • Identificar factores asociados a que el niño tenga alergia.
  • Caso
  • Interpretación
  • Supuestos
  • Evaluación de Supuestos
  • Factores asociados al número de visitas médicas anuales.
md_visit <- import("rwm5yr.dta") %>% 
  characterize()
  • Especificación del modelo
mod <- glm(docvis ~ female + age, 
           family = poisson(link = "log"), 
           data = md_visit)
summary(mod)

Call:
glm(formula = docvis ~ female + age, family = poisson(link = "log"), 
    data = md_visit)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-3.3562  -2.2285  -1.1346   0.3396  26.8860  

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -0.0368083  0.0176597  -2.084   0.0371 *  
female       0.3092910  0.0081168  38.105   <2e-16 ***
age          0.0227500  0.0003624  62.768   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 122270  on 19608  degrees of freedom
Residual deviance: 116363  on 19606  degrees of freedom
AIC: 153636

Number of Fisher Scoring iterations: 6
  • Presentación con intervalos de confianza y exponenciada (OR):
mod %>% 
  tidy(conf.int = TRUE, exponentiate = TRUE)
# A tibble: 3 × 7
  term        estimate std.error statistic p.value conf.low conf.high
  <chr>          <dbl>     <dbl>     <dbl>   <dbl>    <dbl>     <dbl>
1 (Intercept)    0.964  0.0177       -2.08  0.0371    0.931     0.998
2 female         1.36   0.00812      38.1   0         1.34      1.38 
3 age            1.02   0.000362     62.8   0         1.02      1.02

  • female: El número medio de visitas anuales al médico en mujeres fue 20% veces más el de los hombres (RM = 1.33; IC95% 1.31 a 1.35; p < 0.001)

  • age: Por cada incremento de la edad en un año, el número medio de visitas anuales al médico se incrementa en 1% (RM = 1.017; IC95% 1.016 a 1.018; p < 0.001).

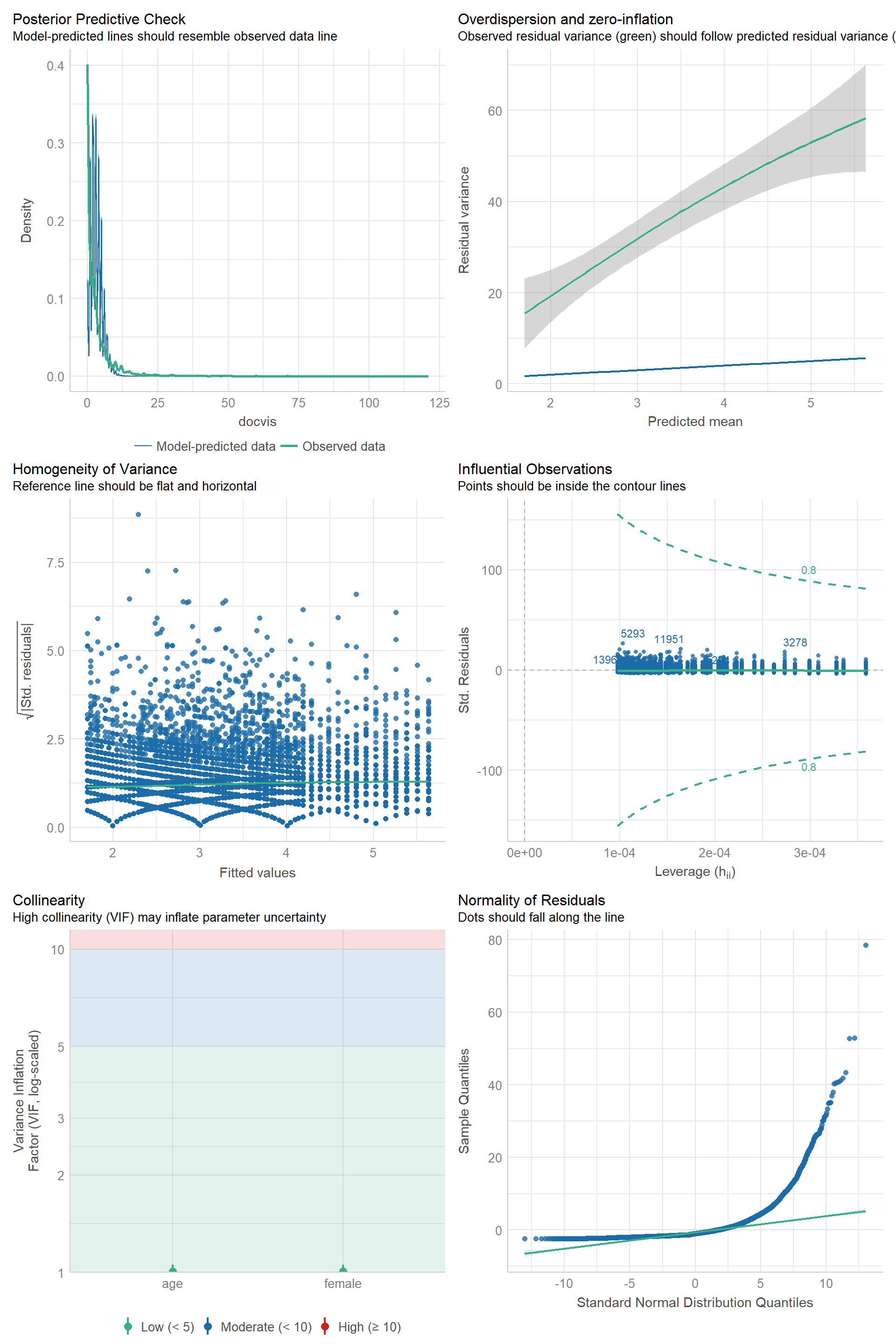
  • Linealidad del log(yi) respecto a la combinación lineal de predictores.

  • Observaciones son independientes.

  • Yi sigue distribución de Poisson.

    • Supuesto de equivarianza.

  • No problemas de regresión:

    • No puntos influyentes

    • No colinealidad: Solo cuando esta es un problema.

  • Supuestos específicos si se busca generalizar a poblaciones conocidas, hacer inferencias causales o ambas.

library(performance)
check_model(mod)

La regresión Binomial Negativa

Agenda

  1. El Modelo Lineal Generalizado

  2. La regresión de Poisson

  3. La regresión Binomial Negativa

  4. Tablas de regresión reproducibles con {gtsummary}

El modelo de regresión binomial negativa

  • Si asumimos que yi tienne un segundo nivel de variabilidad:

yi|λi∼Poisson(λi) y λi∼Gamma(μi,ψ)

  • Entonces, es posible mostrar que yi sigue una distribución binomial negativa.

  • Asimismo, el modelo:

yi∼BN(β0+β1x1i+...+βpxip,ψ)

  • Componente sistemático:

log(E(yi))=ηi

  • Función de enlace:

ηi=β0+β1x1i+...+βpxip

  • Componente aleatorio:

yi∼BN(ηi,ψ)

¿Por qué usar binomial negativa y no poisson?

  • Porque no siempre la variable yi seguirá una distribución de Poisson.

  • Si sigue una distribución BN, entonces la varianza es mayor a la media (sobredispersion).

    • La estimación del error estándar deberá tener esto en cuenta.

    • Caso contrario, sería inválido en dirección anticorservadora.

¿Por qué usar la función de enlace log?

  • La función de enlace de la BN no es log(), tampoco identiy().

  • Sin embargo, se prefiere usar log() para obtener resultados interpretables: razón de medias.

  • Esto conlleva un problema, no siempre hay convergencia:

    • Cuando hay sobredispersión, regresión binomial negativa no siempre es la opción factible.

    • Otra opción puede ser usar regresión quasipoisson o un estimador de varianza robusta.

La regresión BN también retorna razón de medias

  • La regresión BN permite retornar directamente razón de medias (RM).

  • Los coeficientes de regresión β del modelo son log(RM), por lo tanto, podemos exponenciarlos para obtener las RM:

β=log(RM)

entonces

eβ=RM

glm.nb() paso a paso

  • Se usa la función glm.nb() del paquete MASS:
library(MASS)

glm.nb() paso a paso

mod <- glm.nb(docvis ~ female + age, 
           data = md_visit)
summary(mod)

Call:
glm.nb(formula = docvis ~ female + age, data = md_visit, init.theta = 0.4838144807, 
    link = log)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.5688  -1.3167  -0.4629   0.1127   6.5046  

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -0.0366979  0.0457077  -0.803    0.422    
female       0.3370406  0.0222361  15.157   <2e-16 ***
age          0.0224236  0.0009913  22.621   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for Negative Binomial(0.4838) family taken to be 1)

    Null deviance: 21019  on 19608  degrees of freedom
Residual deviance: 20224  on 19606  degrees of freedom
AIC: 85857

Number of Fisher Scoring iterations: 1

              Theta:  0.48381 
          Std. Err.:  0.00659 

 2 x log-likelihood:  -85849.42400
  • Se especifica la ecuación.

glm.nb() paso a paso

mod <- glm.nb(docvis ~ female + age, 
           data = md_visit)
mod %>% 
  tidy() %>% 
  gt()
term estimate std.error statistic p.value
(Intercept) -0.03669795 0.0457077355 -0.8028827 4.220425e-01
female 0.33704062 0.0222361245 15.1573453 6.775303e-52
age 0.02242362 0.0009912903 22.6206366 2.715341e-113
  • En el caso de la función de enlace log, los coeficientes son log(razón de medias), para volverlos interpretables, hay que aplicar antilogaritmo: exp().

glm.nb() paso a paso

mod %>% 
  tidy(exponentiate = TRUE) %>% 
  gt()
term estimate std.error statistic p.value
(Intercept) 0.9639673 0.0457077355 -0.8028827 4.220425e-01
female 1.4007960 0.0222361245 15.1573453 6.775303e-52
age 1.0226769 0.0009912903 22.6206366 2.715341e-113
  • La función tidy() de {broom} permite hacer esto facilmente: exponentiate = TRUE.

glm.nb() paso a paso

mod %>% 
  tidy(exponentiate = TRUE, conf.int = TRUE) %>% 
  gt()
term estimate std.error statistic p.value conf.low conf.high
(Intercept) 0.9639673 0.0457077355 -0.8028827 4.220425e-01 0.8824872 1.053230
female 1.4007960 0.0222361245 15.1573453 6.775303e-52 1.3412238 1.463041
age 1.0226769 0.0009912903 22.6206366 2.715341e-113 1.0207472 1.024612
  • También podemos agregar intervalos de confianza.

Casos aplicado

  • Identificar factores asociados a que el niño tenga alergia.
  • Caso
  • Interpretación
  • Supuestos
  • Evaluación de Supuestos
  • Factores asociados al número de visitas médicas anuales.
md_visit <- import("rwm5yr.dta") %>% 
  characterize()
  • Especificación del modelo
mod <- glm.nb(docvis ~ female + age, 
           data = md_visit)
summary(mod)

Call:
glm.nb(formula = docvis ~ female + age, data = md_visit, init.theta = 0.4838144807, 
    link = log)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.5688  -1.3167  -0.4629   0.1127   6.5046  

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -0.0366979  0.0457077  -0.803    0.422    
female       0.3370406  0.0222361  15.157   <2e-16 ***
age          0.0224236  0.0009913  22.621   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for Negative Binomial(0.4838) family taken to be 1)

    Null deviance: 21019  on 19608  degrees of freedom
Residual deviance: 20224  on 19606  degrees of freedom
AIC: 85857

Number of Fisher Scoring iterations: 1

              Theta:  0.48381 
          Std. Err.:  0.00659 

 2 x log-likelihood:  -85849.42400
  • Presentación con intervalos de confianza y exponenciada (RM):
mod %>% 
  tidy(conf.int = TRUE, exponentiate = TRUE)
# A tibble: 3 × 7
  term        estimate std.error statistic   p.value conf.low conf.high
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>    <dbl>     <dbl>
1 (Intercept)    0.964  0.0457      -0.803 4.22e-  1    0.882      1.05
2 female         1.40   0.0222      15.2   6.78e- 52    1.34       1.46
3 age            1.02   0.000991    22.6   2.72e-113    1.02       1.02

  • female: El número medio de visitas anuales al médico en mujeres fue 20% veces más el de los hombres (RM = 1.40; IC95% 1.34 a 1.46; p < 0.001)

  • age: Por cada incremento de la edad en un año, el número medio de visitas anuales al médico se incrementa en 2.3% (RM = 1.017; IC95% 1.021 a 1.025; p < 0.001).

  • Linealidad del log(yi) respecto a la combinación lineal de predictores.

  • Observaciones son independientes.

  • Yi sigue distribución de Poisson.

    • Supuesto de equivarianza.

  • No problemas de regresión:

    • No puntos influyentes

    • No colinealidad: Solo cuando esta es un problema.

  • Supuestos específicos si se busca generalizar a poblaciones conocidas, hacer inferencias causales o ambas.

library(performance)
check_model(mod)

Tablas de regresión reproducibles con {gtsummary}

Agenda

  1. El Modelo Lineal Generalizado

  2. La regresión de Poisson

  3. La regresión Binomial Negativa

  4. Tablas de regresión reproducibles con {gtsummary}

Tablas de regresión lineal reproducible

  • Podemos usar la librería {gtsummary} para esto.

  • Veamos un ejemplo.

datos <- import("hb.dta") %>% 
  characterize()

Tablas de regresión lineal reproducible

  • Podemos reportar la tabla de regreion multivarible de la siguiente manera:

    • Primero realizamos el modelo:
mod <- lm(hb ~ age + sex, data = datos)
mod %>% 
  tidy(conf.int = TRUE)
# A tibble: 3 × 7
  term        estimate std.error statistic   p.value conf.low conf.high
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>    <dbl>     <dbl>
1 (Intercept)  11.0     0.0505       218.  0          10.9      11.1   
2 age           0.0110  0.000341      32.3 5.81e-218   0.0104    0.0117
3 sex          -0.474   0.0258       -18.3 8.44e- 74  -0.524    -0.423

Tablas de regresión lineal reproducible

  • Se puede crear una tabla de regresión multivariable con la función tbl_regression() de {gtsummary}:
tabla_multi <- mod %>%  
  tbl_regression()

tabla_multi
Characteristic Beta 95% CI1 p-value
age 0.01 0.01, 0.01 <0.001
sex -0.47 -0.52, -0.42 <0.001
1 CI = Confidence Interval

Tablas de regresión lineal reproducible

  • Podemos hacer la tabla de regresiones bivariada con la función tbl_uvregression() de {gtsummary}:
tabla_univ <- datos %>% 
  dplyr::select(age, sex, hb) %>% 
  tbl_uvregression(
    method = lm, 
    y = hb
  ) 

tabla_univ
Characteristic N Beta 95% CI1 p-value
age 10,000 0.01 0.01, 0.01 <0.001
sex 10,000 -0.47 -0.53, -0.42 <0.001
1 CI = Confidence Interval

Tablas de regresión lineal reproducible

  • Luego, podemos fusionar ambas tablas en una sola con la función tbl_merge():
tabla_final <- tbl_merge(list(tabla_univ, tabla_multi), tab_spanner = c("Modelos crudos", "Modelo ajustado")) 

tabla_final
Characteristic Modelos crudos Modelo ajustado
N Beta 95% CI1 p-value Beta 95% CI1 p-value
age 10,000 0.01 0.01, 0.01 <0.001 0.01 0.01, 0.01 <0.001
sex 10,000 -0.47 -0.53, -0.42 <0.001 -0.47 -0.52, -0.42 <0.001
1 CI = Confidence Interval

Tablas de regresión lineal reproducible

  • Podemos exportarlo a MS Word para post-procesamiento y reporte:
tabla_final %>% 
  as_flex_table() %>% 
  save_as_docx(path = "Tabla_Final.docx")

¡Gracias!
¿Preguntas?




https://github.com/psotob91

percys1991@gmail.com

R Aplicado a los Proyectos de Investigación - Sesión 9

1 / 39
Sesión 9 Curso: R Aplicado a los Proyectos de Investigación Percy Soto-Becerra, M.D., M.Sc(c) InkaStats Data Science Solutions | Medical Branch 2022-10-21 https://github.com/psotob91

  1. Slides

  2. Tools

  3. Close
  • Sesión 9
  • El Modelo Lineal Generalizado
  • Modelo Lineal Generalizado
  • Modelo Lineal Generalizado: Anatomía
  • Familia exponencial
  • Estimación de GLM
  • La regresión de Poisson
  • El modelo de regresión de Poisson
  • ¿Por qué usar log?
  • ¿Por qué no asumir normalidad de \(y_i\)?
  • La regresión de Poisson retorna razón de medias
  • glm() paso a paso
  • glm() paso a paso
  • glm() paso a paso
  • glm() paso a paso
  • glm() paso a paso
  • glm() paso a paso
  • glm() paso a paso
  • Casos aplicado
  • La regresión Binomial Negativa
  • El modelo de regresión binomial negativa
  • ¿Por qué usar binomial negativa y no poisson?
  • ¿Por qué usar la función de enlace log?
  • La regresión BN también retorna razón de medias
  • glm.nb() paso a paso
  • glm.nb() paso a paso
  • glm.nb() paso a paso
  • glm.nb() paso a paso
  • glm.nb() paso a paso
  • Casos aplicado
  • Tablas de regresión reproducibles con {gtsummary}
  • Tablas de regresión lineal reproducible
  • Tablas de regresión lineal reproducible
  • Tablas de regresión lineal reproducible
  • Tablas de regresión lineal reproducible
  • Tablas de regresión lineal reproducible
  • Tablas de regresión lineal reproducible
  • ¡Gracias! ¿Preguntas?...
  • https://github.com/psotob91...
  • f Fullscreen
  • s Speaker View
  • o Slide Overview
  • e PDF Export Mode
  • b Toggle Chalkboard
  • c Toggle Notes Canvas
  • d Download Drawings
  • ? Keyboard Help