Sesión 10

Curso: R Aplicado a los Proyectos de Investigación

Percy Soto-Becerra, M.D., M.Sc(c)

InkaStats Data Science Solutions | Medical Branch

2022-10-24

  https://github.com/psotob91

Medidas de frecuencia para datos categóricos

Agenda

  1. Medidas de frecuencia para datos categóricos

  2. Medidas de asociación

  3. Regresión Logística Binaria

  4. Otras regresiones para datos binarios

Probabilidad teórica

La probabilidad es una medida utilizada para evaluar la incertidumbre.

  • Es una medida teórica (desconocida), que queremos estimar.

  • Desde una perspectiva frecuentista, la proporción de eventos en infinitos experimentos aleatorios es una probabilidad.

    • Usamos la proporción observada en la muestra para aproximarnos a la probabilidad teórica.

  • Otra forma de ver la probabildiad es a través de los odds de probabilidad.

Proporción según diseño

  • En un estudio transversal, la probabilidad de tener una enfermedad es su prevalencia.

    • Numerador incluye casos nuevos y antiguos.
    • Denominador es toda la población de interés.

  • En un estudio de cohorte, la probabilidad de desarrollar una enfermedad es su incidencia acumuada (IA).

    • También llamada riesgo absoluto. En jerga epi: riesgo (a secas).
    • Numerador solo inclute casos nuevos.
    • Denominador es población sin evento al inicio del seguimiento.

Proporción

Enfermedad No enfermedad Total
Población a b a + b

Prevalencia

Prev=aa+b

Donde:

a = Casos totales (nuevos y antiguos)

a+b = Toda la población de interés en el punto/periodo de tiempo evaluado.

Incidencia acumulada

IA=aa+b

Donde:

a: Solo incluye casos nuevos durante el seguimeinto.

a+b: Toda la población si y solo sí al inicio todos ellos no tenían la enfermedad.

Prevalencia versus IA

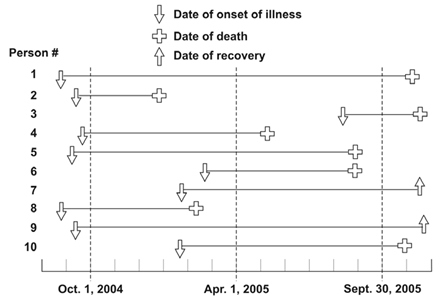
Fuente: Principles of Epidemiology in Public Health Practice, Third Edition An Introduction to Applied Epidemiology and Biostatistics

Odds

  • Sea una variable Y que puede asumir dos valores 1 (ocurre el evento) o 0 (no ocurre el evento).

  • La probabilidad de que ocurra el evento es:

Pr(Y=1)=Número de eventosTotal de observaciones

  • El odds de que ocurra el evento es solo un cambio de escala:

Odds(Y=1)=Pr(Y=1)Pr(Y=0)=Pr(Y=1)1−Pr(Y=1)

Odds (cont.)

  • Los odds son otra forma de presentar a las probabilidades.

  • Mantienen la dirección de su relación con las probabilidades.

  • Cuando las Pr son pequeñas, los Odds≃Pr.

    • Sin embargo, ¡esto no justifica que se interpreten igual!
Pr Odds
0.00 0.0000000
0.01 0.0101010
0.02 0.0204082
0.03 0.0309278
0.04 0.0416667
0.05 0.0526316

Odds versus Probabilidad

  • La probabilidad y el odds no son iguales.

  • Odds diverge de Pr cuando el evento es más frecuente.

0.000.250.500.751.000510152025
PrOdds
plotly-logomark

Interpretación

  • Prevalencia
  • Incidencia

Cuando se estima prevalencia:

Si Pr=0.6 entonces Odds=0.61−0.6=1.5

  • Probabilidad: De cada 100 individuos*, se espera que 60 tengan el evento.

  • Odds: La probabilidad de tener el evento es 1.5 veces la probabilidad de no tenerlo.

(*) En un punto/periodo de tiempo dado.

  • Cuando se estima incidencia acumulada:

Si Pr=0.6 entonces Odds=0.61−0.6=1.5

  • Probabilidad: De cada 100 individuos*, se espera que 60 desarrollen el evento nuevo durante el seguimeinto.

  • Odds: La probabilidad de desearrollar un evento nuevo es 1.5 veces la probabilidad de no desarrollarlo*

(*) En una población que al inicio no tenía el evento.

Diseño de estudio y probabilidad/odds



Indicador Diseño de estudio
Prevalencia Transversal
Incidencia acumulada Cohorte / Ensayo Clínico (EC)
Odds (prevalente) Transversal / Caso-control de casos prevalentes
Odds (incidente) Cohorte/EC/Caso-control de casos incidentes

Medidas de asociación

Agenda

  1. Medidas de frecuencia para datos categóricos

  2. Medidas de asociación

  3. Regresión Logística Binaria

  4. Otras regresiones para datos binarios

Medidas de asociación



  • Podemos comparar las probabilidadesdel desenlace según niveles de otra variable independiente (p. ej., tratamiento, factor de riesgo, etc.).

  • Podemos comparar las probabilidades mediante una resta o mediante una división.

  • Nos centraremos en las medidas de asociación obtenidas mediante división.

Medidas de asociación (resumen)

Medidas de asociación Definición Diseño de estudio
Razón de odds (OR) OR=Odds(Evento|Expuestos)Odds(Evento|No Expuestos)
  • Caso-Control (única medida)
  • Todos los demás
Razón de prevalencias RP=Pr(Evento|Expuestos)Pr(Evento|No Expuestos)
  • Transversal
Razón de riesgos RR=Pr(Evento|Expuestos)Pr(Evento|No Expuestos)

  • Cohorte

  • Ensayo Clínico (EC)

Cálculo de medidas de asociación


  • Los siguientes resultados de un ensayo clínico muestran lo siguiente:
Tratamiento Evento No_evento Total
Placebo 50 950 1000
Tratamiento 25 975 1000

Razón de riesgos

  • La razón de riesgos se calcularía de la siguiente manera:
Tratamiento Evento No_evento Total Calculo_IA Incidencia Calculo_RR RR
Placebo 50 950 1000 50 / 1000 0.050 0.05 / 0.05 1.0
Tratamiento 25 975 1000 25 / 1000 0.025 0.025 / 0.05 0.5
  • RR = 0.5 para Tratamiento.

Interpretación: El riesgo de desarrollar el evento en el grupo tratado fue 50% menor que en el grupo placebo.

Razón de odds

  • La razón de odds (incidente) se calcularía de la siguiente manera:
Tratamiento Evento No_evento Total Calculo_Odds Odds Calculo_OR OR
Placebo 50 950 1000 50 / 950 0.0526316 0.0526 / 0.0526 1.0000000
Tratamiento 25 975 1000 25 / 975 0.0256410 0.0256 / 0.0526 0.4871795
  • OR = 0.49 para Tratamiento.

Interpretación: El odds de desarrollar el evento en el grupo tratado fue 49% menor que en el grupo placebo.

Razón de riesgos y de odds (incidentes)

 

  • Los OR y los RR se aproximan si el evento es poco frecuente.

  • Pero si evento es frecuente, entonces divergen.

  • Por ese motivo, los OR no deben ser interpretados como RR.

0.000.250.500.751.001020
PrOR (red) or RR (blue)
plotly-logomark

Problemas con análisis bivariado


  • ¿Qué pasa si queremos ajustar por otra variable?

  • ¿Qué pasa si no tenemos una variable numérica y queremos relacionarla con el desenlace binario?

  • En ambos casos, podemos realizar un modelo de regresión para datos binarios:

    • Regresión logística binaria

    • Regresión log-binomial

    • Regresión de Poisson modificada

Regresión Logística Binaria

Agenda

  1. Medidas de frecuencia para datos categóricos

  2. Medidas de asociación

  3. Regresión Logística Binaria

  4. Otras regresiones para datos binarios

Anatomía de la Regresión logística binaria

  • Caso específico de Modelo Lineal Generalizado.

  • Componente sistemático:

logit(yi)=log(Odds(yi=1))=log(Pr(yi=1))1−Pr(yi=1))=ηi

  • Función de enlace:

ηi=β0+β1x1i+...+βpxip

  • Componente aleatorio:

yi∼Bernoulli(1,πi)

Regresión logística binaria (cont.)

  • Podemos estimar la Pr(yi=1) a partir del predictor lineal: πi=Pr(yi=1)=eηi1+eηi
  • El modelo es lineal en escala log odds:

  • La ventaja de log odds es que −∞<log(odds)<+∞.
  • Pero no lineal en escala probabilidad:

  • La ventaja es que devuelve un modelo cuya probabiidad predicha está entre 0 y 1.

¿Por qué no usar regresión lineal?

  • Si usamos regresión lineal, el modelo quedaría planetado de esta manera:

E(yi)=Pr(yi=1)=β0+β1x1i+...+βpxip

  • Entonces, el modelo predecirá probabilidades superiores a su rango 0-1:

  • Mientras que regresión logística devolverá probabilidades dentro de rango 0-1:

La controversia del modelo lineal de probabilidad


  • Este modelo es conocido como modelo de probabilidad linear.

    • No es útil para predicción, pero en econometría aún lo usan para explicación.
    • El problema es que la validez del error estándar solo ocurre bajo ciertas condiciones. Es mejor usar modelos más apropiados.

  • Algunos artículos:

https://pubmed.ncbi.nlm.nih.gov/31218050/

https://academic.oup.com/aje/article-abstract/123/1/174/49113?redirectedFrom=fulltext&login=false

https://academic.oup.com/aje/article/162/3/199/171116

La controversia del modelo lineal de probabilidad

I stopped for a reason ;). Some folks have recently tried to re-introduce the "linear probability model". I'm sure it doesn't mean the end of the world if you use lpm's but I'm not too impressed (so far). Why? I like odds ratios and I like my probabilities between 0 and 1

— Maarten van Smeden (@MaartenvSmeden) January 30, 2020

https://pubmed.ncbi.nlm.nih.gov/31218050/

La regresión logística retorna OR

  • La regresión logística permite retonar directamente razón de odds (OR).

  • Los coeficientes de regresión β del modelo son log(OR), por lo tanto, podemos exponenciarlos para obtener los OR:

β=log(OR)

entonces

eβ=OR

Casos aplicado 1

  • Objetivo
  • OR e IC95%
  • Interpretación
  • Supuestos
  • check_model
  • Linealidad
  • Bernoulli
  • Punt. Influy.

  • Factores asociados a desarrollo de alergia en niños.

  • Especificación del modelo

mod <- glm(allergyc ~ smokem + smokef + allergym + allergyf, 
           family = binomial(link = "logit"), 
           data = datos_allergy)
summary(mod)

Call:
glm(formula = allergyc ~ smokem + smokef + allergym + allergyf, 
    family = binomial(link = "logit"), data = datos_allergy)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.2345  -0.9159  -0.7282   1.3215   1.9142  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  -1.6577     0.1480 -11.204  < 2e-16 ***
smokem        0.4714     0.1477   3.191 0.001418 ** 
smokef        0.5401     0.1416   3.813 0.000137 ***
allergym      0.4657     0.1434   3.248 0.001161 ** 
allergyf      0.3137     0.1356   2.314 0.020694 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 1386.9  on 1124  degrees of freedom
Residual deviance: 1338.5  on 1120  degrees of freedom
AIC: 1348.5

Number of Fisher Scoring iterations: 4
mod %>% 
  tidy(conf.int = TRUE, exponentiate = TRUE) %>% 
  gt()
term estimate std.error statistic p.value conf.low conf.high
(Intercept) 0.1905801 0.1479590 -11.203667 3.911979e-29 0.1417981 0.2533683
smokem 1.6022634 0.1477348 3.190968 1.417968e-03 1.2007109 2.1435105
smokef 1.7162328 0.1416441 3.813301 1.371229e-04 1.3013358 2.2681936
allergym 1.5930869 0.1433559 3.248374 1.160666e-03 1.2030369 2.1110603
allergyf 1.3684143 0.1355733 2.313528 2.069365e-02 1.0486014 1.7845927

  • smokem: El odds de desarrollar alergia en niños de madres fumadoras es 1.6 veces el de niños de madres no fumadoras, controlando por antecedente de fumar de padre, alergia de madre y alergia de padre (OR = 1.6; IC95% 1.20 a 2.14; p < 0.001).

  • smokef: El odds de desarrollar alergia en niños de papás fumadoras es 1.72 veces el de niños de papás no fumadoras, controlando por antecedente de fumar de madre, alergia de madre y alergia de padre (OR = 1.72; IC95% 1.30 a 2.27; p = 0.001.

  • allergym: El odds de desarrollar alergia en niños de madres con alergias es 1.59 veces el de niños de madres sin alergia, controlando por antecedente de fumar de madre, antecedente de fumar del papá, y alergia del papá (OR = 1.59; IC95% 1.20 a 2.11; p = 0.001).

  • allergyf: El odds de desarrollar alergia en niños de papás con alergias es 1.37 veces el de niños de papás sin alergia, controlando por antecedente de fumar de madre, antecedente de fumar del papá, y alergia de la madre (OR = 1.37; IC95% 1.05 a 1.78; p = 0.021).

  • Linealidad del logit(yi=1) respecto a los predictores.

  • Observaciones son independientes.

  • Yi sigue distribución de bernoulli.

  • No problemas de regresión:

    • No puntos influyentes

    • No colinealidad: Solo cuando esta es un problema.

  • Panel de check_model será poco informativo. Es mejor usar otras funciones.
check_model(mod)

  • Todas las covariables son categóricas, por lo que la linealidad no es un problema en este modelo.
library(statmod)
set.seed(2134)
quant_res <- qresid(mod)
ggqqplot(quant_res)

library(car)
influenceIndexPlot(mod)

Casos aplicado 2

  • Objetivo
  • OR e IC95%
  • Interpretación
  • Supuestos
  • check_model
  • Linealidad
  • Bernoulli
  • Punt. Influy.

  • Factores asociados a tener lumbalgia a 5 años de seguimeinto.

  • Especificación del modelo

mod <- glm(bp5 ~ bp0 + sex + age + phyocc + social, 
           family = binomial(link = "logit"), 
           data = datos_backpain)
summary(mod)

Call:
glm(formula = bp5 ~ bp0 + sex + age + phyocc + social, family = binomial(link = "logit"), 
    data = datos_backpain)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-0.8376  -0.6390  -0.5445  -0.4522   2.2500  

Coefficients:
                    Estimate Std. Error z value Pr(>|z|)    
(Intercept)         -2.32105    0.66735  -3.478 0.000505 ***
bp0                 -0.07754    0.20862  -0.372 0.710123    
sexfemale            0.37870    0.16619   2.279 0.022684 *  
age                  0.01291    0.01446   0.893 0.371905    
phyocc2 - low       -0.46094    0.31224  -1.476 0.139875    
phyocc3 - moderate  -0.03143    0.28279  -0.111 0.911501    
phyocc4 - heavy      0.44284    0.31320   1.414 0.157385    
socialself employed -0.25900    0.23512  -1.102 0.270657    
socialwhite collar  -0.01484    0.21221  -0.070 0.944266    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 992.22  on 1123  degrees of freedom
Residual deviance: 971.86  on 1115  degrees of freedom
  (195 observations deleted due to missingness)
AIC: 989.86

Number of Fisher Scoring iterations: 4
library(broom)
mod %>% 
  tidy(conf.int = TRUE, exponentiate = TRUE, ) 
# A tibble: 9 × 7
  term                estimate std.error statistic  p.value conf.low conf.high
  <chr>                  <dbl>     <dbl>     <dbl>    <dbl>    <dbl>     <dbl>
1 (Intercept)           0.0982    0.667    -3.48   0.000505   0.0261     0.358
2 bp0                   0.925     0.209    -0.372  0.710      0.607      1.38 
3 sexfemale             1.46      0.166     2.28   0.0227     1.06       2.03 
4 age                   1.01      0.0145    0.893  0.372      0.985      1.04 
5 phyocc2 - low         0.631     0.312    -1.48   0.140      0.343      1.17 
6 phyocc3 - moderate    0.969     0.283    -0.111  0.912      0.564      1.72 
7 phyocc4 - heavy       1.56      0.313     1.41   0.157      0.853      2.92 
8 socialself employed   0.772     0.235    -1.10   0.271      0.481      1.21 
9 socialwhite collar    0.985     0.212    -0.0699 0.944      0.650      1.50

  • bp0: El odds de tener dolor lumbar crónico en quienes reportaron antecedente de lumbalgia fue 7% menor que en quienes negaron antecedente de lumbalgia, luego de controlar por sexo, edad, nivel de actividad física y estatus social. Sin embargo, no se cuenta con suficiente evidencia estadística para concluir que la asociación exista en la población debido a la gran imprecisión de la estimación (OR = 0.93; 95%CI 0.61 a 1.38, p = 0.710).

  • sex: El odds de tener dolor lumbar crónica en mujeres fue 1.46 veces el de varones, luego de controlar por antecedente de lumbalgia, edad, nivel de actividad física y estatus social (OR = 1.46; 95%CI 1.06 a 2.03; p = 0.023).

  • age: El aumento en un año de edad se asocia a un aumento de 1.3% de los odds de tener dolor lumbar crónico, luego de controlar por sexo, antecedente de lumbalgia, nivel de actividad física y estatus social (OR = 1.01; 95%CI 0.98 a 1.04; p = 0.372). Teniendo en cuenta la incertidumbre de la estimación, no podemos afirmar si esta relación existe en la población.

  • phyocc - low: El odds de tener dolor lumbar crónico en quienes reportan niveles bajos de actividad física es 37% menor que en quienes reportan niveles de actividad física muy bajos, luego de controlar por sexo, antecedente de lumbalgia, edad y estatus social (OR = 0.63; 95%CI 0.34 a 1.17; p = 0.140). La gran varibabilidad muestral previene que podamos afirmar la existencia de una relación en la población.

  • phyocc - moderate: El odds de tener dolor lumbar crónico en quienes reportan niveles moderados de actividad física es 3% menor que en quienes reportan niveles de actividad física muy bajos, luego de controlar por sexo, antecedente de lumbalgia, edad y estatus social (OR = 0.97; 95%CI 0.56 a 1.72; p = 0.912). Teniendo en cuenta la incertidumbre de la estimación, no podemos afirmar si esta relación existe en la población.

  • phyocc - heavy: El odds de tener dolor lumbar crónico en quienes reportan niveles intensos de actividad física es 1.56 veces mayor que en quienes reportan niveles de actividad física muy bajos, luego de controlar por sexo, antecedente de lumbalgia, edad y estatus social (OR = 1.56; 95%CI 0.85 a 2.92; p = 0.157). Teniendo en cuenta la incertidumbre de la estimación, no podemos afirmar si esta relación existe en la población.

  • socialself employed: [completar]

  • socialwhite collar: [completar]

  • Linealidad del logit(yi=1) respecto a los predictores.

  • Observaciones son independientes.

  • Yi sigue distribución de bernoulli.

  • No problemas de regresión:

    • No puntos influyentes

    • No colinealidad: Solo cuando esta es un problema.

  • Panel de check_model será poco informativo.
library(performance)
check_model(mod)

library(ggeffects)
pr <- ggpredict(mod, "age [all]")
plot(pr, residuals = TRUE, residuals.line = TRUE)

library(statmod)
set.seed(2134)
quant_res <- qresid(mod)
ggqqplot(quant_res)

library(car)
influenceIndexPlot(mod)

Otras regresiones para datos binarios

Agenda

  1. Medidas de frecuencia para datos categóricos

  2. Medidas de asociación

  3. Regresión Logística Binaria

  4. Otras regresiones para datos binarios

RR / RP versus OR

  • RR o RP son más interpretables a nivel clínico o de Salud Pública.

  • Cuando el evento es frecuente, interpretar odds como probabilidades ocasiona una sobreestimación de las probabilidades.

    • A un RR de 1.2 le puede corresponder un OR de 5. (¿cuál medida es la mejor?)

  • Sin embargo, es un problea de interpretación.

    • Si se interpreta apropiadamente, el OR no es malo en sí.

  • El OR es fácil de estimar mediante una regresión logística.

  • Sin embargo, si se desea estimar RR / RP, entonces debemos cambiar el enfoque de modelado.

¿Cómo estimar RR / RP?

  • Hay varios enfoques.

    • Puede derivarse RR/RP de OR obtenidos mediante regresión logística.

    • También podemos usar métodos de sobrevida.

  • En investigación clínica o epidemiológica, comúnmente se usan estos dos enfoques:

    • Regresión log-binomial

    • Regresión de Poisson modificada.

Modelo de regresión log-binomial


  • Similar estructura que regresión logística (modelo logit-binomial).

  • Asume que Yi sigue una distribución de bernoulli (caso particular de binomial).

  • Cambia la función de enlace logit() por log(), lo que retorna probabilidades, ya no odds.

Regresión log-binomial: Anatomía

Componente sistemático:

log(E(Y|x1i,...,xpi))=log(E(Yi))=ηi=β0+β1x1i+...+βpxip

  • log() es la función de enlace logaritmo nepereano.

  • ηi es el predictor linear.

  • Función de enlace:

ηi=β0+β1x1i+...+βpxip

  • Componente aleatorio:

yi∼Bernoulli(1,πi)

Estimación de probabilidad

  • Podemos estimar la Pr(yi=1) a partir del predictor lineal:

πi=Pr(yi=1)=eηi

La regresión log-binomial retorna RR/RP

  • La regresión log-binomial permite retonar directamente razón de prevalencias (RP) o razón de incidencias acumuladas (RR) dependiendo del diseño.

  • Los coeficientes de regresión β del modelo son log(RR) o log(RP), por lo tanto, podemos exponenciarlos para obtener los RR o RR:

Estudio transversal

β=log(RP)

entonces

eβ=RP

Estudio de cohortes

eβ=RR

entonces

β=log(RR)

  • Asimismo, si el modelo es correcto la inferencia (valor p e IC95%) debería ser válida.

Problemas con la regresión log-binomial


  • Usa una función de enlace no canónica para la distibución binomial

  • Esto significa que no siempre se garantiza la convergencia del modelo.

  • Si esto ocurre, debemos optar por un modelo que sí converga:

    • Regresión de Poisson modificada

Modelo de regresión Poisson modificado


  • Similar estructura que regresión logística (modelo logit-binomial) y que el modelo log-binomial.

  • Aunque modelo de regresión de Poisson asume que Yi sigue una distribución de Poisson, se lo modifica para que este supuesto no importe.

  • Cambia la función de enlace logit() por log(), lo que retorna probabilidades, ya no odds.

Regresión Poisson modificado: Anatomía

  • Su estructura es la misma que el modelo de regresión de Poisson:

Componente sistemático:

log(E(Y|x1i,...,xpi))=log(E(Yi))=ηi=β0+β1x1i+...+βpxip

  • log() es la función de enlace logaritmo nepereano.

  • ηi es el predictor linear.

  • Función de enlace:

ηi=β0+β1x1i+...+βpxip

  • Podemos estimar la Pr(yi=1) a partir del predictor lineal:

πi=Pr(yi=1)=eηi

  • Componente aleatorio:

yi∼Poisson(λ=πi)

  • Modificación del modelo:

    • Para estimar apropiadamente la varianza de los β y tener inferencias válidas (valor p e IC95% apropiados), el modelo aplica una estimación robusta de varianza tipo sandwich.

La regresión de Poisson también retorna RR/RP

  • La regresión de Poisson permite retonar directamente razón de prevalencias (RP) o razón de incidencias acumuladas (RR) dependiendo del diseño.

  • Los coeficientes de regresión β del modelo son log(RR) o log(RP), por lo tanto, podemos exponenciarlos para obtener los RR o RR:

Estudio transversal

β=log(RP)

entonces

eβ=RP

Estudio de cohortes

β=log(RP)

entonces

eβ=RR

  • Sin embargo, si el modelo es correcto la inferencia no es válida salvo que se corrija la varianza.

    • Ajuste robusto de varianza es opción más usada.

Casos aplicados

  • Identificar factores asociados a que el niño tenga alergia.
  • Ejemplo 1
  • Ejemplo 2

  • Factores asociados a desarrollo de alergia en niños.

  • Especificación del modelo

mod <- glm(allergyc ~ smokem + smokef + allergym + allergyf, 
           family = poisson(link = "log"), 
           data = datos_allergy)
summary(mod)

Call:
glm(formula = allergyc ~ smokem + smokef + allergym + allergyf, 
    family = poisson(link = "log"), data = datos_allergy)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.0643  -0.8186  -0.6807   0.7641   1.3707  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  -1.7689     0.1247 -14.181  < 2e-16 ***
smokem        0.3181     0.1217   2.613  0.00899 ** 
smokef        0.3687     0.1178   3.130  0.00175 ** 
allergym      0.3066     0.1146   2.674  0.00749 ** 
allergyf      0.2070     0.1096   1.888  0.05904 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 815.58  on 1124  degrees of freedom
Residual deviance: 782.50  on 1120  degrees of freedom
AIC: 1482.5

Number of Fisher Scoring iterations: 5
  • Presentación con intervalos de confianza y exponenciada (RR):
library(broom)
library(sandwich)
mod %>% 
  tidy(conf.int = TRUE, exponentiate = TRUE, vcov = sandwich) 
# A tibble: 5 × 7
  term        estimate std.error statistic  p.value conf.low conf.high
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>    <dbl>     <dbl>
1 (Intercept)    0.171     0.125    -14.2  1.21e-45    0.133     0.217
2 smokem         1.37      0.122      2.61 8.99e- 3    1.08      1.75 
3 smokef         1.45      0.118      3.13 1.75e- 3    1.15      1.82 
4 allergym       1.36      0.115      2.67 7.49e- 3    1.08      1.70 
5 allergyf       1.23      0.110      1.89 5.90e- 2    0.991     1.52

  • Interpretación:

    • smokem: El riesgo de desarrollar alergia en niños de madres fumadoras es 1.37 veces el de niños de madres no fumadoras, controlando por antecedente de fumar de padre, alergia de madre y alergia de padre (RR = 1.37; IC95% 1.08 a 1.75; p < 0.001).

    • smokef: El riesgo de desarrollar alergia en niños de papás fumadoras es 1.45 veces el de niños de papás no fumadoras, controlando por antecedente de fumar de madre, alergia de madre y alergia de padre (RR = 1.45; IC95% 1.15 a 1.82; p = 0.009).

    • allergym: El riesgo de desarrollar alergia en niños de madres con alergias es 1.36 veces el de niños de madres sin alergia, controlando por antecedente de fumar de madre, antecedente de fumar del papá, y alergia del papá (RR = 1.36; IC95% 1.08 a 1.70; p = 0.007).

    • allergyf: El riesgo de desarrollar alergia en niños de papás con alergias es 1.23 veces el de niños de papás sin alergia, controlando por antecedente de fumar de madre, antecedente de fumar del papá, y alergia de la madre (RR = 1.23; IC95% 0.99 a 1.52; p = 0.059).

Supuestos

  • Linealidad del logit(yi=1) respecto a los predictores.

  • Observaciones son independientes.

  • Yi sigue distribución de bernoulli.

  • No problemas de regresión:

    • No puntos influyentes

    • No colinealidad: Solo cuando esta es un problema.

library(performance)
check_model(mod)

  • Factores asociados a tener lumbalgia a 5 años de seguimeinto.

  • Especificación del modelo

mod <- glm(bp5 ~ bp0 + sex + age + phyocc + social, 
           family = poisson(link = "log"), 
           data = datos_backpain)
summary(mod)

Call:
glm(formula = bp5 ~ bp0 + sex + age + phyocc + social, family = poisson(link = "log"), 
    data = datos_backpain)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-0.7792  -0.6056  -0.5246  -0.4424   1.7811  

Coefficients:
                     Estimate Std. Error z value Pr(>|z|)    
(Intercept)         -2.381838   0.606973  -3.924  8.7e-05 ***
bp0                 -0.064393   0.189777  -0.339   0.7344    
sexfemale            0.313311   0.151318   2.071   0.0384 *  
age                  0.010589   0.013120   0.807   0.4196    
phyocc2 - low       -0.397751   0.288867  -1.377   0.1685    
phyocc3 - moderate  -0.025682   0.258255  -0.099   0.9208    
phyocc4 - heavy      0.357670   0.283432   1.262   0.2070    
socialself employed -0.213537   0.214439  -0.996   0.3194    
socialwhite collar  -0.009969   0.192679  -0.052   0.9587    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 661.07  on 1123  degrees of freedom
Residual deviance: 644.08  on 1115  degrees of freedom
  (195 observations deleted due to missingness)
AIC: 1024.1

Number of Fisher Scoring iterations: 6
  • Presentación con intervalos de confianza y exponenciada (RP):
library(sandwich)
mod %>% 
  tidy(conf.int = TRUE, exponentiate = TRUE, vcov = sandwich) 
# A tibble: 9 × 7
  term                estimate std.error statistic   p.value conf.low conf.high
  <chr>                  <dbl>     <dbl>     <dbl>     <dbl>    <dbl>     <dbl>
1 (Intercept)           0.0924    0.607    -3.92   0.0000870   0.0276     0.299
2 bp0                   0.938     0.190    -0.339  0.734       0.637      1.34 
3 sexfemale             1.37      0.151     2.07   0.0384      1.02       1.85 
4 age                   1.01      0.0131    0.807  0.420       0.985      1.04 
5 phyocc2 - low         0.672     0.289    -1.38   0.169       0.383      1.20 
6 phyocc3 - moderate    0.975     0.258    -0.0994 0.921       0.598      1.65 
7 phyocc4 - heavy       1.43      0.283     1.26   0.207       0.832      2.54 
8 socialself employed   0.808     0.214    -0.996  0.319       0.523      1.22 
9 socialwhite collar    0.990     0.193    -0.0517 0.959       0.678      1.44

  • Interpretación:

    • bp0: La prevalencia de tener dolor lumbar crónico en quienes reportaron antecedente de lumbalgia fue 6% menor que en quienes negaron antecedente de lumbalgia, luego de controlar por sexo, edad, nivel de actividad física y estatus social. Sin embargo, no se cuenta con suficiente evidencia estadística para concluir que la asociación exista en la población debido a la gran imprecisión de la estimación (RP = 0.94; 95%CI 0.64 a 1.34, p = 0.734).

    • sex: La prevalencia de tener dolor lumbar crónica en mujeres fue 1.37 veces el de varones, luego de controlar por antecedente de lumbalgia, edad, nivel de actividad física y estatus social (RP = 1.37; 95%CI 1.02 a 1.85; p = 0.038).

    • age: El aumento en un año de edad se asocia a un aumento de 1.1% de la prevalencia de tener dolor lumbar crónico, luego de controlar por sexo, antecedente de lumbalgia, nivel de actividad física y estatus social (RP = 1.01; 95%CI 0.99 a 1.04; p = 0.420). Teniendo en cuenta la incertidumbre de la estimación, no podemos afirmar si esta relación existe en la población.

    • phyocc - low: La prevalencia de tener dolor lumbar crónico en quienes reportan niveles bajos de actividad física es 33% menor que en quienes reportan niveles de actividad física muy bajos, luego de controlar por sexo, antecedente de lumbalgia, edad y estatus social (RP = 0.38; 95%CI 0.34 a 1.20; p = 0.169). La gran varibabilidad muestral previene que podamos afirmar la existencia de una relación en la población.

    • phyocc - moderate: La prevalencia de tener dolor lumbar crónico en quienes reportan niveles moderados de actividad física es 3% menor que en quienes reportan niveles de actividad física muy bajos, luego de controlar por sexo, antecedente de lumbalgia, edad y estatus social (RP = 0.97; 95%CI 0.60 a 1.65; p = 0.921). Teniendo en cuenta la incertidumbre de la estimación, no podemos afirmar si esta relación existe en la población.

    • phyocc - heavy: La prevalencia de tener dolor lumbar crónico en quienes reportan niveles intensos de actividad física es 1.43 veces mayor que en quienes reportan niveles de actividad física muy bajos, luego de controlar por sexo, antecedente de lumbalgia, edad y estatus social (RP = 1.43; 95%CI 0.83 a 2.54; p = 0.207). Teniendo en cuenta la incertidumbre de la estimación, no podemos afirmar si esta relación existe en la población.

    • socialself employed: [completar]

    • socialwhite collar: [completar]

Supuestos

  • Linealidad del logit(yi=1) respecto a los predictores.

  • Observaciones son independientes.

  • Yi sigue distribución de bernoulli.

  • No problemas de regresión:

    • No puntos influyentes

    • No colinealidad: Solo cuando esta es un problema.

library(performance)
check_model(mod)

¡Gracias!
¿Preguntas?




https://github.com/psotob91

percys1991@gmail.com

R Aplicado a los Proyectos de Investigación - Sesión 10

1 / 42
Sesión 10 Curso: R Aplicado a los Proyectos de Investigación Percy Soto-Becerra, M.D., M.Sc(c) InkaStats Data Science Solutions | Medical Branch 2022-10-24 https://github.com/psotob91

  1. Slides

  2. Tools

  3. Close
  • Sesión 10
  • Medidas de frecuencia para datos categóricos
  • Probabilidad teórica
  • Proporción según diseño
  • Proporción
  • Prevalencia versus IA
  • Odds
  • Odds (cont.)
  • Odds versus Probabilidad
  • Interpretación
  • Diseño de estudio y probabilidad/odds
  • Medidas de asociación
  • Medidas de asociación
  • Medidas de asociación (resumen)
  • Cálculo de medidas de asociación
  • Razón de riesgos
  • Razón de odds
  • Razón de riesgos y de odds (incidentes)
  • Problemas con análisis bivariado
  • Regresión Logística Binaria
  • Anatomía de la Regresión logística binaria
  • Regresión logística binaria (cont.)
  • ¿Por qué no usar regresión lineal?
  • La controversia del modelo lineal de probabilidad
  • La controversia del modelo lineal de probabilidad
  • La regresión logística retorna OR
  • Casos aplicado 1
  • Casos aplicado 2
  • Otras regresiones para datos binarios
  • RR / RP versus OR
  • ¿Cómo estimar RR / RP?
  • Modelo de regresión log-binomial
  • Regresión log-binomial: Anatomía
  • Estimación de probabilidad
  • La regresión log-binomial retorna RR/RP
  • Problemas con la regresión log-binomial
  • Modelo de regresión Poisson modificado
  • Regresión Poisson modificado: Anatomía
  • La regresión de Poisson también retorna RR/RP
  • Casos aplicados
  • ¡Gracias! ¿Preguntas?...
  • https://github.com/psotob91...
  • f Fullscreen
  • s Speaker View
  • o Slide Overview
  • e PDF Export Mode
  • b Toggle Chalkboard
  • c Toggle Notes Canvas
  • d Download Drawings
  • ? Keyboard Help